tugassains.com – Vektor adalah salah satu konsep dasar dalam fisika dan matematika yang memiliki arah dan besar. Dalam dunia nyata, vektor digunakan untuk merepresentasikan berbagai fenomena seperti kecepatan, gaya, dan perpindahan. Salah satu operasi penting pada vektor adalah pengurangan vektor, yang sering kali muncul dalam analisis masalah ilmiah dan teknik.
Artikel ini akan membahas pengertian pengurangan vektor, cara melakukannya secara grafis dan analitis, serta menyajikan contoh soal pengurangan vektor yang dapat membantu Anda memahami konsep ini secara mendalam.
Apa Itu Pengurangan Vektor?
Pengurangan vektor adalah proses menghitung selisih antara dua vektor. Dalam matematika, pengurangan vektor dapat dianggap sebagai penjumlahan vektor dengan arah yang berlawanan. Artinya, jika Anda ingin mengurangkan vektor BBB dari vektor AAA, Anda cukup menjumlahkan AAA dengan negatif dari BBB.
Secara matematis, pengurangan vektor dinyatakan sebagai: C = A − B
Di mana C adalah vektor hasil pengurangan, A adalah vektor pertama, dan B adalah vektor kedua.
Cara Melakukan Pengurangan Vektor
Ada dua cara utama untuk melakukan pengurangan vektor:
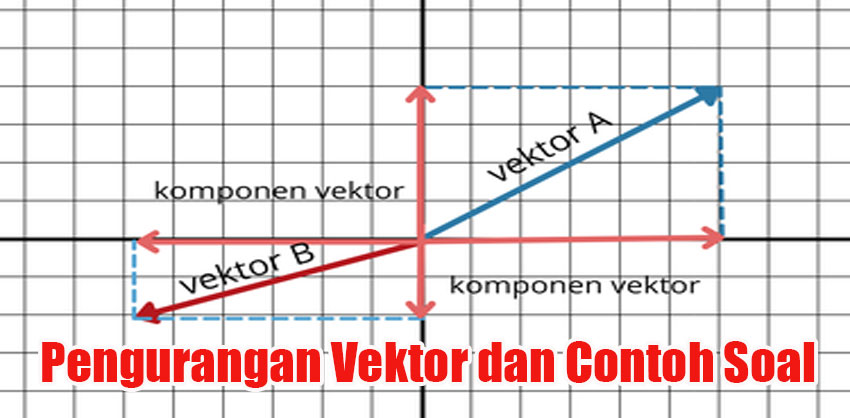
1. Secara Grafis
Pengurangan vektor secara grafis dilakukan dengan menggambar vektor −B (vektor B dengan arah berlawanan) dan kemudian menjumlahkannya dengan A menggunakan metode head-to-tail.
2. Secara Analitis
Dalam metode analitis, pengurangan vektor dilakukan dengan mengurangkan komponen-komponen vektor secara langsung dalam sumbu x, y, dan z (jika ada). Rumusnya adalah:
Cx = Ax − Bx
Cy = Ay − By
Cz = Az − Bz
Di mana Ax, Ay, Az, adalah komponen vektor A, dan Bx, By, Bz adalah komponen vektor B.
Baca juga: Perkalian Skalar Vektor dan Contoh Soal
Contoh Soal Pengurangan Vektor
Contoh Soal 1: Pengurangan Vektor Secara Grafis
Dua vektor diberikan sebagai berikut:
- A : 5 satuan dengan arah ke kanan (sumbu x).
- B : 3 satuan dengan arah ke kiri (sumbu x).
Langkah-langkah:
- Gambarkan vektor A sejajar dengan sumbu x ke arah kanan.
- Gambarkan −B sebagai vektor sejajar sumbu x, tetapi ke arah kanan (karena negatif dari arah B adalah ke kanan).
- Gabungkan ujung A dengan ujung −B.
Hasil:
- Panjang hasil pengurangan adalah 5 − 3 = 2 satuan.
- Arah hasil pengurangan adalah ke kanan.
Contoh Soal 2: Pengurangan Vektor Secara Analitis di 2D
Dua vektor diberikan dalam bentuk komponen:
- A = ( 6,4 )
- B = ( 3,7 )
Hitung hasil pengurangan A − B.
Langkah-langkah:
- Kurangi komponen x: Cx = 6 − 3
- Kurangi komponen y: Cy = 4 − 7 = −3
Hasil: Vektor hasil pengurangan adalah: C = (3, − 3)
Contoh Soal 3: Pengurangan Vektor Secara Analitis di 3D
Diberikan dua vektor dalam tiga dimensi:
- A = ( 8, −5,7 )
- B = ( 3,2, −4 )
Hitung hasil pengurangan A − B.
Langkah-langkah:
- Kurangi komponen x: Cx = 8 −3 = 5
- Kurangi komponen y: Cy=−5 −2= −7
- Kurangi komponen z: Cz= 7− (−4) = 7+4 = 11
Hasil: Vektor hasil pengurangan adalah: C= ( 5, −7, 11 )
Baca juga: Perkalian Titik Dua Vektor: Rumus dan Contoh Soal
Aplikasi Pengurangan Vektor dalam Kehidupan Nyata
- Analisis Gaya dalam Fisika
Pengurangan vektor sering digunakan untuk menghitung resultan gaya yang bekerja pada suatu benda ketika dua gaya berlawanan diterapkan. - Navigasi
Dalam navigasi, pengurangan vektor digunakan untuk menentukan posisi relatif atau jarak antar objek bergerak. - Perpindahan dalam Geografi
Ketika menghitung perpindahan antara dua titik di permukaan bumi, pengurangan vektor dapat digunakan untuk mendapatkan hasil yang akurat.
Pengurangan vektor adalah operasi penting yang sering digunakan dalam analisis fisika dan matematika. Baik dilakukan secara grafis maupun analitis, pengurangan vektor membantu kita memahami hubungan antara arah dan besaran vektor yang berbeda. Dengan memahami cara melakukan pengurangan vektor dan mempraktikkannya melalui contoh soal pengurangan vektor, Anda dapat menguasai konsep ini dengan lebih baik.
Untuk informasi lebih lanjut tentang operasi vektor lainnya, seperti penjumlahan, perkalian, atau proyeksi vektor, kunjungi artikel kami tentang “operasi dasar vektor dalam fisika dan matematika“.