Bilangan Kompleks, Memahami Dunia Angka yang Lebih Luas

tugassains.com – Ketika berbicara tentang angka, kebanyakan dari kita hanya mengenal bilangan real seperti 1, -3, atau 2.5. Namun, ada jenis angka lain yang memainkan peran penting dalam matematika modern, fisika, teknik, hingga komputer sains, yaitu bilangan kompleks. Artikel ini akan membahas apa itu bilangan kompleks, sifat-sifatnya, bagaimana cara mengoperasikannya, dan contoh penggunaannya dalam kehidupan nyata.

Apa Itu Bilangan Kompleks?

Bilangan kompleks adalah angka yang terdiri dari dua komponen utama: bagian real dan bagian imajiner. Bentuk umum bilangan kompleks dapat dituliskan sebagai:

z = a + bi

Di mana:

• a adalah bagian real (bilangan real biasa seperti 2, -5, atau 0.7).
• b adalah bagian imajiner (bilangan real yang dikalikan dengan iii, yaitu akar dari -1).

Simbol i disebut unit imajiner dan didefinisikan sebagai:

i²=−1

Contoh Bilangan Kompleks

• 3 + 4i : Bagian real adalah 3, bagian imajiner adalah 4.
• −5i : Bagian real adalah 0, bagian imajiner adalah -5.
• 7 : Bagian real adalah 7, bagian imajiner adalah 0.

Sejarah Singkat Bilangan Kompleks

Bilangan kompleks muncul dari kebutuhan untuk menyelesaikan persamaan kuadrat yang hasilnya adalah bilangan negatif di bawah tanda akar.

Pada abad ke-16, matematikawan Italia, Rafael Bombelli, menjadi orang pertama yang merumuskan aturan bilangan ini. Meskipun pada awalnya dianggap tidak memiliki arti fisik, bilangan kompleks kemudian ditemukan memiliki aplikasi luas di berbagai bidang sains dan teknologi.

Operasi Matematika dengan Bilangan Kompleks

1. Penjumlahan dan Pengurangan

Penjumlahan dan pengurangan dilakukan dengan menggabungkan bagian real dan bagian imajiner secara terpisah.

Contoh:

( 3 + 4i ) + ( 2 −i ) = 5 + 3i

( 5 + 3i ) − ( 1 + 2i ) = 4 + i

2. Perkalian

Perkalian menggunakan aturan distributif dengan memperhatikan bahwa i² = − 1.

Contoh:

( 2 + 3i ) ( 1 − 4i ) = 2 − 8i + 3i −12i² = 14 − 5i

3. Pembagian

Pembagian melibatkan konjugasi bilangan kompleks.

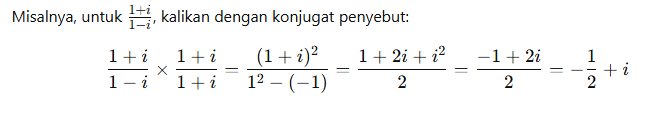
Baca juga: Contoh Soal Menentukan Harga Bilangan Oksidasi

Sifat-Sifat Penting Bilangan Kompleks

1. Konjugat Kompleks
   Konjugat kompleks dari z = a + bi adalah zˉ=a−bi. Konjugat ini sering digunakan dalam pembagian bilangan kompleks.
2. Modulus Bilangan Kompleks
   Modulus adalah panjang dari bilangan kompleks saat direpresentasikan pada bidang kompleks. Didefinisikan sebagai:

3. Representasi Polar

Bilangan kompleks juga bisa ditulis dalam bentuk polar:

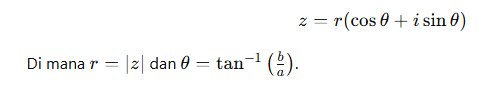
Aplikasi Bilangan Kompleks dalam Kehidupan Nyata

1. Listrik dan Elektronik

Bilangan kompleks digunakan untuk merepresentasikan arus listrik dan tegangan dalam bentuk impedansi (resistansi total dalam rangkaian AC). Bagian real menggambarkan resistansi, sementara bagian imajiner menggambarkan reaktansi.

2. Sinyal dan Pemrosesan Data

Dalam pemrosesan sinyal, bilangan kompleks digunakan untuk menganalisis frekuensi sinyal menggunakan transformasi Fourier. Ini penting dalam teknologi komunikasi seperti radio, TV, dan internet.

3. Grafik dan Animasi Komputer

Dalam grafik komputer, bilangan kompleks sering digunakan untuk menghasilkan fraktal, pola matematika yang kompleks seperti Set Mandelbrot.

4. Fisika Kuantum

Bilangan kompleks menjadi dasar dalam persamaan Schrödinger, yang menggambarkan perilaku partikel dalam mekanika kuantum.

5. Matematika Keuangan

Bilangan kompleks digunakan dalam model stokastik untuk menghitung opsi dan analisis risiko di pasar keuangan.

Bilangan Kompleks dalam Bidang Pendidikan

Memahami bilangan kompleks adalah langkah penting bagi siswa yang belajar matematika tingkat lanjut. Topik ini sering dianggap sulit, tetapi dengan pendekatan yang benar, bilangan kompleks justru menjadi alat yang sangat menarik untuk menjelaskan konsep-konsep yang lebih mendalam.

Strategi Pembelajaran:

1. Gunakan Visualisasi
   Representasi bilangan kompleks di bidang kompleks (sumbu x untuk bagian real, sumbu y untuk bagian imajiner) membantu siswa memahami operasi dasar.
2. Berikan Contoh Praktis
   Siswa lebih mudah memahami konsep jika diberikan aplikasi nyata, seperti perhitungan impedansi dalam listrik.

Baca juga: Pengurangan Vektor dan Contoh Soal

Bilangan kompleks adalah konsep matematika yang luar biasa dan memiliki berbagai aplikasi praktis dalam dunia nyata. Dengan memahami operasi, sifat, dan penerapannya, kita bisa membuka pintu ke berbagai bidang ilmu pengetahuan dan teknologi.

Jadi, jangan ragu untuk memperdalam pemahaman Anda tentang bilangan kompleks dan kegunaannya. Siapa tahu, pengetahuan ini bisa membantu Anda dalam memecahkan masalah kompleks yang tampak mustahil di dunia nyata.

Tertarik belajar lebih jauh? Nantikan artikel kami berikutnya tentang “cara menggunakan bilangan kompleks dalam pemrograman Python untuk pemrosesan sinyal”!