Rumus Titik Berat Benda: Konsep, Cara Menghitung, dan Contoh Praktis

tugassains.com – Dalam fisika, titik berat adalah konsep penting yang digunakan untuk memahami distribusi massa suatu benda. Pemahaman tentang rumus titik berat benda tidak hanya penting bagi pelajar, tetapi juga bagi insinyur, arsitek, dan profesi lain yang berkaitan dengan perancangan struktur atau mesin. Artikel ini akan membahas konsep, rumus, cara menghitung, serta penerapan titik berat dengan penjelasan unik dan mendalam.

Apa Itu Titik Berat?

Titik berat adalah titik di mana seluruh massa benda dianggap terpusat. Dalam situasi gravitasi seragam, titik berat juga dikenal sebagai pusat gravitasi. Secara sederhana, titik berat adalah tempat di mana benda bisa seimbang jika ditopang.

Contoh sederhana: Bayangkan Anda mencoba menyeimbangkan penggaris di ujung jari. Titik tempat penggaris tidak jatuh ke sisi mana pun adalah titik beratnya.

Rumus Titik Berat Benda

Titik berat benda ditentukan oleh distribusi massa dan posisi benda tersebut. Rumus umum untuk menghitung titik berat dalam sistem koordinat kartesian adalah:

Cara Menghitung Titik Berat

Berikut adalah langkah-langkah untuk menghitung titik berat benda:

1. Identifikasi bentuk dan distribusi massa benda:
   Tentukan apakah benda tersebut berbentuk sederhana (persegi, lingkaran, segitiga) atau kompleks (gabungan beberapa bentuk).
2. Pilih sistem koordinat:
   Letakkan sistem koordinat di sekitar benda untuk mempermudah penghitungan.
3. Bagi benda menjadi bagian kecil (jika kompleks):
   Untuk benda yang terdiri dari beberapa bagian, hitung massa dan posisi masing-masing bagian.
4. Gunakan rumus:
   Masukkan nilai x_i, y_i​, dan m_i​ ke dalam rumus untuk menghitung X_c, dan Yc​.

Contoh Perhitungan Titik Berat

1. Titik Berat Sebuah Persegi Panjang

Misalkan Anda memiliki persegi panjang dengan panjang 10 cm dan lebar 5 cm. Massa benda dianggap seragam. Karena distribusi massa simetris, titik beratnya berada tepat di tengah:

Titik beratnya berada di (5 cm, 2.5 cm).

2. Titik Berat Benda Gabungan

Misalkan benda terdiri dari dua persegi panjang:

• Persegi panjang pertama (A): panjang 8 cm, lebar 4 cm, massa 2 kg
• Persegi panjang kedua (B): panjang 6 cm, lebar 3 cm, massa 1 kg

Koordinat pusat masing-masing:

• Titik berat A: (4 cm, 2 cm)
• Titik berat B: (3 cm, 1.5 cm)

Gunakan rumus:

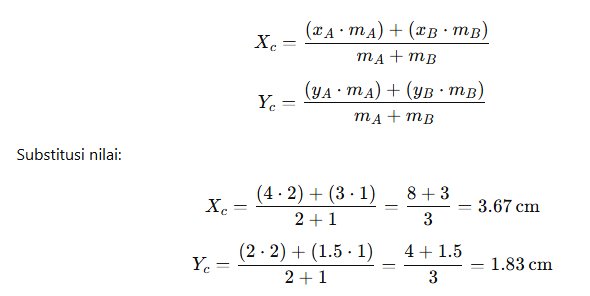
Titik berat gabungan adalah (3.67 cm, 1.83 cm).

Penerapan Titik Berat dalam Kehidupan Sehari-Hari

1. Perancangan Kendaraan:
   Dalam desain mobil atau pesawat, titik berat sangat penting untuk memastikan stabilitas dan performa. Titik berat yang terlalu tinggi dapat menyebabkan kendaraan terbalik.
2. Struktur Bangunan:
   Arsitek menggunakan titik berat untuk memastikan bahwa gedung tidak mudah goyah, terutama saat terkena angin kencang atau gempa.
3. Olahraga:
   Dalam olahraga seperti senam atau yoga, atlet menggunakan konsep titik berat untuk menyeimbangkan tubuh.
4. Pengangkutan Barang:
   Saat memuat barang di truk, titik berat harus diperhatikan agar kendaraan tidak kehilangan keseimbangan saat bergerak.

Kesalahan Umum dalam Menghitung Titik Berat

1. Mengabaikan distribusi massa yang tidak seragam:
   Banyak benda memiliki massa yang tidak tersebar merata. Ini harus diperhatikan agar hasil pengukuran akurat.
2. Tidak mempertimbangkan sumbu koordinat yang tepat:
   Salah memilih sistem koordinat bisa membuat perhitungan menjadi rumit atau bahkan salah.
3. Melewatkan detail benda kecil dalam benda gabungan:
   Untuk benda kompleks, setiap bagian kecil harus dihitung.

Mengapa Penting Memahami Rumus Titik Berat Benda?

Memahami konsep titik berat benda membantu kita dalam banyak aspek kehidupan. Dari mengemudi kendaraan hingga membuat desain, konsep ini memastikan efisiensi dan keamanan. Bagi pelajar, titik berat juga menjadi dasar untuk memahami konsep lanjutan dalam fisika seperti momen gaya dan keseimbangan.

Baca juga: Jenis-jenis Keseimbangaan Benda

Titik berat benda adalah topik penting yang mengajarkan kita bagaimana massa suatu benda terdistribusi. Dengan memahami rumus titik berat benda dan cara menghitungnya, kita dapat menerapkan konsep ini dalam berbagai aspek kehidupan. Mulailah dari objek sederhana untuk belajar, dan terapkan konsep ini pada benda yang lebih kompleks untuk memperluas pemahaman Anda.

Ingin belajar lebih lanjut? Baca artikel kami berikutnya tentang “cara menghitung momen inersia benda dengan distribusi massa tidak seragam” untuk memperdalam pengetahuan Anda tentang fisika mekanika!

Pada umumnya titik berat benda gabungan tersebut diperoleh dengan menghitung nilai titik berat pusat dari gabungan-gabungan dengan proses tertentu.