Perkalian titik dua vektor (dot product) adalah salah satu operasi dasar dalam aljabar vektor yang sering digunakan dalam berbagai bidang ilmu, seperti fisika, matematika, dan teknik. Operasi ini menghasilkan nilai skalar dari dua vektor yang diperbanyak, berbeda dengan perkalian silang yang menghasilkan vektor baru. Dalam artikel ini, kita akan membahas “perkalian titik dua vektor” secara mendalam, mulai dari pengertian, rumus, hingga penerapannya dalam kehidupan nyata.
Apa Itu Perkalian Titik Dua Vektor?
Perkalian titik dua vektor adalah operasi matematis yang menghitung hasil kali proyeksi satu vektor pada arah vektor lainnya. Hasilnya adalah skalar, yang berarti tidak memiliki arah, hanya nilai. Operasi ini berguna untuk memahami hubungan antara dua vektor, terutama dalam menentukan besar sudut atau mengukur kerja mekanis dalam fisika.
Secara matematis, perkalian titik dua vektor dapat ditulis sebagai:

Rumus Perkalian Titik Dua Vektor
Ada dua cara utama untuk menghitung perkalian titik dua vektor:
1. Berdasarkan Sudut Antara Vektor
Jika panjang vektor A dan B diketahui, serta sudut di antara keduanya ( θ ), gunakan rumus:
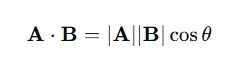
2. Berdasarkan Komponen Vektor
Jika kedua vektor A dan B diberikan dalam bentuk komponen seperti:
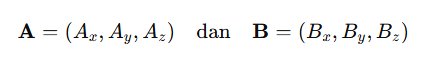
maka perkalian titiknya dihitung sebagai:
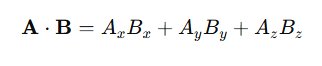
Contoh Soal Perkalian Titik Dua Vektor
Contoh 1: Menggunakan Sudut Antar Vektor
Dua vektor memiliki panjang |A|=5 dan |B|=3, serta sudut di antara keduanya adalah 60∘. Hitung perkalian titik dua vektor tersebut.
Penyelesaian:
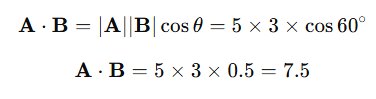
Hasilnya adalah 7.5.
Contoh 2: Menggunakan Komponen Vektor
Dua vektor dinyatakan sebagai:
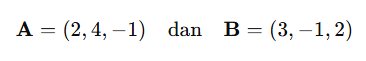
Hitung perkalian titik dua vektor tersebut.
Penyelesaian:
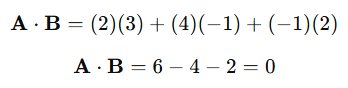
Hasilnya adalah 000, yang berarti kedua vektor saling tegak lurus (90∘).
Baca juga: Panjang Vektor: Rumus dan Contoh Soal
Aplikasi Perkalian Titik Dua Vektor
Perkalian titik dua vektor memiliki banyak aplikasi, terutama dalam bidang:
1. Fisika
Kerja Mekanis: Dalam fisika, kerja mekanis dihitung menggunakan dot product antara gaya (F) dan perpindahan (d):
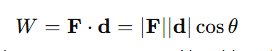
Hasilnya menunjukkan besarnya energi yang dikerahkan dalam perpindahan.
2. Komputer Grafik
Dalam grafik komputer, dot product digunakan untuk menentukan intensitas cahaya yang jatuh pada suatu objek, dengan menghitung sudut antara vektor cahaya dan permukaan objek.
3. Geometri
Dot product digunakan untuk menentukan apakah dua vektor saling tegak lurus ( A ⋅ B = 0 ) atau untuk mencari sudut di antara keduanya.
4. Teknik Mesin dan Teknik Elektro
Dalam teknik, dot product berguna untuk menghitung aliran energi, seperti daya listrik atau tenaga yang dikerahkan mesin.
Keunggulan Perkalian Titik Dua Vektor
- Mudah Dihitung: Dengan metode komponen, hitungannya sederhana dan cepat.
- Interpretasi Fisik yang Jelas: Dot product memberikan wawasan yang intuitif tentang hubungan dua vektor, seperti sudut atau besaran kerja.
- Penerapan Luas: Operasi ini digunakan di berbagai disiplin ilmu.
Baca juga: Vektor Satuan: Rumus dan Contoh Soal
Perkalian titik dua vektor adalah operasi matematis fundamental yang menghasilkan skalar dari dua vektor. Dengan memahami konsep ini, kita dapat mengaplikasikannya dalam berbagai bidang, mulai dari fisika, geometri, hingga grafik komputer. Rumus perkalian titik dua vektor tidak hanya relevan untuk menyelesaikan masalah teknis, tetapi juga membantu kita memahami hubungan antara berbagai vektor di ruang tiga dimensi.
Jika Anda ingin mempelajari lebih lanjut, baca artikel kami berikutnya tentang “perbedaan perkalian titik dan silang vektor”, yang akan membantu memperluas wawasan Anda tentang aljabar vektor!



