Momen inersia adalah konsep penting dalam fisika, khususnya dalam mekanika rotasi. Momen inersia menggambarkan resistansi sebuah benda terhadap perubahan kecepatan sudutnya saat berputar. Ketika massa benda terdistribusi secara tidak seragam, perhitungan momen inersia menjadi lebih kompleks tetapi juga menarik karena menantang kita untuk memahami distribusi massa dalam ruang tiga dimensi.
Pada artikel ini, kita akan membahas secara mendalam cara menghitung momen inersia untuk benda dengan distribusi massa tidak seragam. Mulai dari konsep dasar hingga contoh konkret, Anda akan mendapatkan wawasan lengkap yang dapat diterapkan dalam kehidupan sehari-hari maupun bidang akademik.
Apa Itu Momen Inersia?
Secara matematis, momen inersia didefinisikan sebagai:

Bagi benda dengan distribusi massa seragam, dmdmdm dapat diestimasi dengan mudah berdasarkan densitas rata-rata. Namun, jika distribusi massa tidak seragam, maka dmdmdm harus dihitung berdasarkan fungsi distribusi massa.
Langkah-Langkah Menghitung Momen Inersia Benda dengan Distribusi Massa Tidak Seragam
1. Pahami Geometri dan Sumbu Rotasi Benda
Langkah pertama adalah memahami bentuk geometris benda dan posisi sumbu rotasi. Misalnya, apakah benda berbentuk silinder, bola, atau lembaran datar? Sumbu rotasi bisa berada di pusat, ujung, atau bahkan di luar benda.
2. Identifikasi Distribusi Massa Benda
Distribusi massa tidak seragam biasanya dinyatakan dalam bentuk fungsi densitas massa, seperti:

3. Bagilah Benda ke dalam Elemen Massa Kecil
Pisahkan benda menjadi elemen massa kecil (dm) yang lebih mudah dihitung. Elemen ini biasanya dinyatakan dalam bentuk:

4. Tentukan Jarak dari Sumbu Rotasi
Hitung jarak elemen massa kecil (rrr) dari sumbu rotasi. Untuk geometri sederhana, rrr bisa berupa jarak radial. Namun, untuk benda kompleks, rrr harus dihitung berdasarkan posisi relatif elemen massa terhadap sumbu.
5. Integrasikan Momen Inersia
Substitusi elemen massa kecil (dm) ke dalam rumus momen inersia:
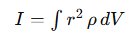
Selanjutnya, lakukan integrasi dengan batas sesuai dimensi benda (panjang, luas, atau volume).
Baca juga: Jenis-jenis Keseimbangaan Benda
Contoh Perhitungan Momen Inersia: Batang dengan Densitas Variabel
Misalkan sebuah batang panjang L memiliki distribusi massa tidak seragam yang dinyatakan sebagai:

1. Elemen Massa Kecil (dm)

2. Momen Inersia terhadap Sumbu di Ujung Kiri ( x = 0 )

Aplikasi Momen Inersia dengan Distribusi Massa Tidak Seragam
- Desain Teknik Mesin: Momen inersia digunakan dalam merancang roda gigi, turbin, dan poros mesin.
- Konstruksi Bangunan: Menentukan kekuatan struktural balok yang memiliki distribusi beban tidak merata.
- Astronomi: Menghitung rotasi planet yang memiliki distribusi massa heterogen.
- Robotika: Meningkatkan stabilitas robot dengan perhitungan momen inersia dari komponen-komponennya.
Baca juga: Rumus Titik Berat Benda: Konsep, Cara Menghitung, dan Contoh Praktis
Menghitung momen inersia untuk benda dengan distribusi massa tidak seragam membutuhkan pemahaman geometri, densitas massa, dan teknik integrasi. Meskipun kompleks, pendekatan ini sangat penting dalam berbagai bidang teknik, fisika, dan astronomi. Dengan mempraktikkan langkah-langkah yang dijelaskan di atas, Anda dapat menguasai konsep ini dan mengaplikasikannya secara efektif.
Jangan ragu untuk mencoba perhitungan pada geometri lain, seperti bola atau silinder, untuk lebih memahami bagaimana distribusi massa memengaruhi momen inersia. Selamat belajar!