Memahami rumus keliling lingkaran sangat penting dalam matematika, terutama bagi pelajar yang sedang mempelajari geometri. Lingkaran adalah bentuk yang sering kita jumpai sehari-hari, baik di roda kendaraan, jam dinding, atau bahkan piring makan. Dengan mengetahui cara menghitung keliling lingkaran, kita bisa lebih memahami bentuk-bentuk di sekitar kita dan penerapannya dalam dunia nyata.
Dalam artikel ini, kita akan membahas cara menghitung keliling lingkaran menggunakan rumus yang tepat, membedah komponen dari lingkaran, serta memberikan beberapa contoh soal yang bisa membantu memperdalam pemahaman Anda tentang topik ini.
Pengertian Lingkaran dan Keliling
Lingkaran adalah himpunan semua titik dalam bidang yang berjarak sama dari titik tertentu yang disebut titik pusat. Sedangkan keliling lingkaran adalah panjang garis yang mengelilingi lingkaran tersebut. Untuk memahami rumusnya, kita perlu mengetahui dua istilah penting:
- Diameter (d): Jarak garis lurus yang menghubungkan dua titik pada lingkaran melalui titik pusatnya.
- Jari-jari (r): Jarak dari titik pusat lingkaran ke titik mana pun pada lingkaran.
Keliling lingkaran bisa dihitung dengan rumus keliling lingkaran sederhana yang menggunakan jari-jari atau diameter lingkaran tersebut.
Rumus Keliling Lingkaran
Ada dua cara menghitung keliling lingkaran berdasarkan apakah Anda memiliki panjang diameter atau jari-jari lingkaran. Keduanya menggunakan konstanta matematika yang dikenal sebagai π (Pi), yang mendekati 3,14159.
Rumus Keliling Lingkaran Menggunakan Diameter: K = π × d
Di mana:
- K adalah keliling lingkaran
- d adalah diameter lingkaran
Rumus Keliling Lingkaran Menggunakan Jari-Jari: K = 2 × π × r
Di mana:
- K adalah keliling lingkaran
- r adalah jari-jari lingkaran
Kedua rumus di atas sama-sama benar dan digunakan sesuai dengan informasi yang dimiliki.
Baca juga: Jumlah Suku ke-n Barisan Aritmatika
Contoh Soal Keliling Lingkaran
Berikut adalah beberapa contoh soal yang dapat membantu Anda memahami cara menggunakan rumus keliling lingkaran.
Contoh Soal 1: Menghitung Keliling Lingkaran dengan Diameter
Sebuah roda sepeda memiliki diameter 28 cm. Berapakah keliling roda tersebut?
Penyelesaian:
- Diketahui: diameter d = 28 cm
- Rumus: K = π × d
Jadi, keliling roda sepeda adalah 87,92 cm.
Contoh Soal 2: Menghitung Keliling Lingkaran dengan Jari-Jari
Sebuah piring memiliki jari-jari 14 cm. Hitunglah keliling piring tersebut.
Penyelesaian:
- Diketahui: jari-jari r = 14 cm
- Rumus: K = 2 × π × r
K = 2 × 3, 14 × 14 = 87,92 cm
Keliling piring tersebut adalah 87,92 cm.
Contoh Soal 3: Menghitung Jari-Jari dari Keliling Lingkaran
Jika sebuah lingkaran memiliki keliling 31,4 cm, berapakah panjang jari-jari lingkaran tersebut?
Penyelesaian:
- Diketahui: keliling K = 31,4 cm
- Rumus: K = 2 × π × r
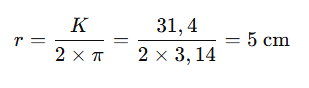
Jadi, panjang jari-jari lingkaran tersebut adalah 5 cm.
Baca juga: Cara Mencari Rasio Deret Geometri
Pentingnya Menguasai Rumus Keliling Lingkaran
Dalam banyak bidang, mulai dari desain teknik hingga arsitektur, mengetahui keliling lingkaran sangat penting.
Misalnya, seorang insinyur perlu menghitung keliling roda gigi atau struktur lingkaran lainnya. Di dunia pendidikan, rumus keliling lingkaran membantu siswa memahami konsep pengukuran keliling dan memperkenalkan konsep konstanta matematika π. Selain itu, rumus ini juga menjadi dasar bagi perhitungan luas lingkaran.
Kesalahan Umum dalam Menghitung Keliling Lingkaran
Beberapa kesalahan yang sering terjadi saat menghitung keliling lingkaran antara lain:
- Salah mengidentifikasi diameter dan jari-jari: Penting untuk membedakan antara diameter dan jari-jari, karena diameter adalah dua kali panjang jari-jari.
- Menggunakan nilai π yang salah: Jika presisi dibutuhkan, gunakan nilai π lebih mendetail (misalnya 3,14159 atau 22/7).
- Lupa menambahkan satuan pada jawaban: Hasil penghitungan keliling harus disertai satuan, misalnya cm, meter, atau kilometer.
Baca juga: Contoh Soal Barisan Aritmatika Beserta Pembahasan
Rumus Lanjutan Terkait Lingkaran
Selain rumus keliling, ada juga rumus lain yang sering dipelajari dalam konteks lingkaran, seperti:
Rumus Luas Lingkaran: L = π × r2
Luas lingkaran berguna untuk mengetahui ruang dalam lingkaran tersebut, misalnya luas lantai pada struktur bangunan berbentuk lingkaran.
Rumus Sudut Lingkaran
Jika Anda menghitung bagian tertentu dari lingkaran (misalnya dalam sektor atau segmen), Anda akan menggunakan sudut dalam radian atau derajat untuk menentukan proporsi dari lingkaran penuh.
π (Pi) adalah konstanta yang berasal dari perbandingan antara keliling lingkaran dan diameternya. Nilainya selalu sekitar 3,14159, yang membuatnya menjadi konstanta yang digunakan secara universal dalam perhitungan yang melibatkan lingkaran.
Baca juga: Memahami Lambang Miu (μ) dalam Fisika: Fungsi, Makna, dan Aplikasinya
Rumus keliling lingkaran adalah konsep dasar yang penting dalam matematika dan geometri. Memahami cara menghitung keliling dapat membantu Anda dalam berbagai aplikasi nyata, mulai dari mengukur jarak melingkar hingga memahami konsep-konsep penting dalam sains. Dengan latihan dan pemahaman yang mendalam, Anda akan bisa mengaplikasikan konsep keliling lingkaran ini di berbagai bidang kehidupan.
Ingin mempelajari lebih lanjut? Kunjungi artikel kami yang lain tentang rumus luas lingkaran dan contoh aplikasinya untuk pemahaman yang lebih menyeluruh mengenai perhitungan dalam geometri!



