Dalam fisika, konsep vektor memainkan peran penting dalam memahami fenomena alam, terutama yang melibatkan gerak, gaya, dan berbagai besaran fisik lainnya. Vektor adalah besaran yang memiliki besar (magnitude) dan arah, berbeda dengan besaran skalar yang hanya memiliki besar. Operasi vektor dalam fisika mencakup berbagai manipulasi matematika, seperti penjumlahan, pengurangan, perkalian, dan dekomposisi. Artikel ini akan membahas beberapa operasi vektor dasar dan aplikasinya dalam dunia fisika.
1. Penjumlahan dan Pengurangan Vektor
Operasi dasar pada vektor adalah penjumlahan dan pengurangan. Penjumlahan vektor dapat dilakukan dengan dua cara: metode paralelogram dan metode segitiga.
Metode Paralelogram
Jika dua vektor A dan B diwakili oleh dua sisi dari sebuah paralelogram yang dimulai dari titik yang sama, maka vektor hasilnya adalah diagonal dari paralelogram tersebut. Ini menggambarkan bagaimana dua vektor dapat dijumlahkan secara grafis.
Metode Segitiga
Penjumlahan vektor juga bisa dilakukan dengan menghubungkan ujung pangkal vektor pertama dengan ujung pangkal vektor kedua, dan hasilnya adalah garis dari pangkal awal ke ujung akhir dari vektor kedua.
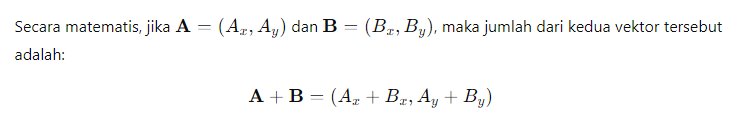
Pengurangan vektor, sebaliknya, dapat dianggap sebagai penjumlahan vektor dengan arah yang berlawanan.
Baca juga: Besaran Skalar dan Besaran Vektor dalam Fisika
2. Perkalian Vektor
Ada dua jenis perkalian vektor dalam fisika: perkalian skalar (dot product) dan perkalian silang (cross product).
Perkalian Skalar (Dot Product): Operasi ini menghasilkan sebuah skalar. Misalkan ada dua vektor A dan B, maka perkalian skalar mereka dinyatakan sebagai:
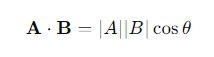
di mana |A| dan |B| adalah besar dari masing-masing vektor, dan θ adalah sudut antara kedua vektor. Perkalian skalar digunakan untuk menghitung pekerjaan (work) yang dilakukan oleh suatu gaya dalam arah tertentu.
Perkalian Silang (Cross Product): Operasi ini menghasilkan sebuah vektor baru yang tegak lurus terhadap kedua vektor asal. Rumus perkalian silang dua vektor A dan B adalah:
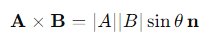
di mana n adalah vektor satuan yang tegak lurus terhadap bidang yang dibentuk oleh A dan B. Perkalian silang sering digunakan dalam fisika untuk menghitung momen gaya (torque) atau medan magnetik.
Baca juga: Buku Paket Fisika Kelas 10 Kurikulum Merdeka
3. Dekomposisi Vektor
Dekomposisi vektor adalah proses memecah vektor menjadi komponen-komponennya, biasanya sepanjang sumbu kartesian (x, y, dan z). Ini sangat penting dalam analisis fisika karena banyak masalah melibatkan lebih dari satu dimensi.
Misalnya, sebuah vektor F dengan besar dan arah tertentu dapat diuraikan menjadi komponen-komponennya sebagai:
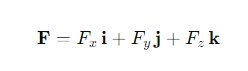
di mana i, j, k adalah vektor satuan sepanjang sumbu x, y, dan z.
Baca juga: Proyeksi Skalar dan Proyeksi Vektor Ortogonal
4. Aplikasi Operasi Vektor dalam Fisika
Operasi vektor sangat penting dalam berbagai cabang fisika. Berikut adalah beberapa aplikasi kunci:
Mekanika
Dalam mekanika klasik, vektor digunakan untuk menggambarkan posisi, kecepatan, dan percepatan benda. Misalnya, hukum kedua Newton F = ma menyatakan bahwa gaya (vektor) yang bekerja pada suatu benda sama dengan massa benda dikalikan dengan percepatannya (juga vektor).
Elektromagnetisme
Dalam elektromagnetisme, medan listrik dan medan magnet digambarkan sebagai vektor. Persamaan Maxwell, yang merupakan dasar dari elektromagnetisme, menggunakan operasi vektor seperti gradien, divergensi, dan rotasi.
Dinamika Fluida
Aliran fluida digambarkan dengan vektor kecepatan, dan banyak analisis dinamika fluida bergantung pada operasi vektor untuk memahami pergerakan fluida dalam ruang.
Baca juga: Vektor Satuan: Rumus dan Contoh Soal
Pemahaman tentang operasi vektor adalah kunci untuk memahami banyak konsep dasar dalam fisika. Dengan menguasai operasi-operasi ini, seperti penjumlahan, pengurangan, perkalian, dan dekomposisi, kita dapat mengembangkan pemahaman yang lebih baik tentang bagaimana dunia fisik bekerja.
Baik dalam mekanika, elektromagnetisme, maupun dinamika fluida, operasi vektor memberikan alat yang diperlukan untuk analisis yang akurat dan pemodelan matematis dari fenomena alam.
Dengan demikian, operasi vektor tidak hanya merupakan dasar dari banyak perhitungan fisika tetapi juga menjadi fondasi bagi perkembangan teknologi dan ilmu pengetahuan di berbagai bidang.