tugassains.com – Barisan aritmatika merupakan bilangan berpola didalam matematika yang memiliki pola selisih antara suatu suku dengan suku sebelumnya memiliki nilai yang selalu tetap.
Melalui artikel ini kita akan belajar mengenai Barisan Aritmatika dengan contoh soal yang disertai pembahasan sebagai bahan belajar berikut.

Baca Juga Contoh Soal Deret Geometri
Contoh Soal Barisan Aritmatika
1. Hitunglah besar nilai beda dari 1, 3, 5, 7, 9, …!
Penyelesaian:
Hitung besar beda barisan aritmatika yaitu besar selisih antara suatu suku dengan suku sebelumnya, kita akan hitung selisih pada suku ke-2 (U2 = 3) dengan suku ke-1 (U1 = 1).
b = U2 – U1
b = 3 – 1
b = 2
Jadi besar nilai beda yaitu 2.
2. Hitunglah berapa besar suku ke-5 dan suku ke-6 dari suatu barisan 5, 11, 17, 23, …?
penyelesaian:
Hitung besar beda kemudian cari nilai U5 dan U6.
b = U2 – U1
b = 11 – 5
b = 6
Cari nilai suku ke-5 dan ke-6 dengan menggunakan rumus suku ke-n barisan aritmatika (a = 5 dan b = 6)
Un = a + (n – 1)b
U5 = 5 + (5 – 1)6
= 5 + (4)6
= 29
U5 = 5 + (6 – 1)6
= 5 + (5)6
= 35
Jadi berturut-turut nilai suku ke-5 dan suku ke-6 yaitu U5 = 29 dan U6 = 35.
3. Apabila suatu barisan aritmatika memiliki suku pertama bernilai 7 dengan besar beda bernilai 5 berapa besar suku ke-7?
penyelesaian:
Dengan nilai a = 7 dan b = 5 kemudian hitung besar nilai suku ke-7.
Un = a + (n – 1)b
U7 = 7 + (7 – 1)5
= 7 + (6)5
= 7 + 30
= 37
Jadi besar suku ke-7 bernilai 37.
4. Seorang insinyur ingin memasang penanda batas jalan yang dimulai pada titik 9 kilometer dan dipasang secara berjarak 3 kilometer antara lampu dengan lampu selanjutnya. Apabila insinyur hanya memiliki 15 lampu yang akan dipasang, maka sejauh mana insinyur dapat memasang lampu?
penyelesaian:
Permasalahan tersebut merupakan permisalan dari bentuk barisan aritmatika yaitu titik awal atau a = 9 kemudian jarak atau beda b = 3 kemudian kita akan mencari letak titik ke-15 dengan rumus suku ke-n.
Un = a + (n – 1)b
U15 = 9 + (15 – 1)3
U15 = 9 + (14)3
U15 = 9 + 42
U15 = 51
Jadi insinyur tersebut dapat memasang lampu sejauh pada titik 51 kilometer.
5. Carilah suku tengah dari barisan 7, 14, 21, …, 126, 133 dan cari terletak pada suku ke berapa!
penyelesaian: Mencari suku tengah barisan aritmatika (Ut) dilakukan dengan menjumlahkan suku pertama (a = 7) dengan suku terakhir (Un = 157) pada barisan kemudian bagi dengan dua.
Ut = (a + Un) / 2
Ut = (7 + 133) / 2
= (140) / 2
= 70
Kemudian cari letak suku tengah dengan subtitusi ke dalam rumus suku ke-n.
Un = a + (n – 1)b
70 = 7 + (n – 1)7
70 = 7 + 7n – 7
70 = 7n
n = 7
Jadi besar suku tengah bernilai 70 terletak pada suku ke-7.
5. Berapakah besar S8 dari 2, 8, 14, 20, ….?
penyelesaian: nilai S8 merupakan jumlah suku ke-n barisan aritmatika, dengan nilai a = 2 selanjutnya cari terlebih dahulu nilai b dan hitung hasilnya.
b = U2 – U1
b = 8 – 2
b = 6
Sn = n/2 × (2a + (n – 1)b)
S8 = 8/2 × (2(2) + (8 – 1)6)
= 4 × (4 + (7)6)
= 4 × (4 + 42)
= 4 × 46
= 184
Jadi nilai S8 = 184.
6. Carilah jumlah suku ke-15 dari barisan aritmatika apabila memiliki suku pertama 9 dan beda sebesar 3!
penyelesaian: mencari jumlah suku ke-n barisan aritmatika dapat di
Sn = n/2 × (2a + (n – 1)b)
S15 = 15/2 × (2(9) + (15 – 1)3)
= 15/2 × (18 + (14)3)
= 15/2 × (18 + 42)
= 15/2 × 60
= 450
Jadi jumlah suku ke-15 sebesar 450.
7. Carilah besar suku pertama (a) dan beda barisan (b) pada barisan aritmatika apabila diketahui nilai jumlah suku ke-4 bernilai 36 dan jumlah suku ke-8 bernilai 136!
penyelesaian: Untuk mencari nilai a dan b kita dapat mencari dengan mesubtitusikan terlebih dahulu ke dalam rumus.
Sn = n/2 × (2a + (n – 1)b)
S4 = 4/2 × (2a + (4 – 1)b)
36 = 2 × (2a + 3b)
36 = 4a + 6b …(1)
S8 = 8/2 × (2a + (8 – 1)b)
136 = 4 × (2a + 7b)
136 = 8a + 28b …(2)
Selanjutnya lakukan metode eliminasi spldv dari persamaan untuk mencari nilai b.
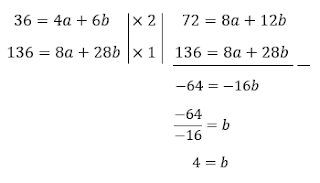
kemudian lakukan subtitusi nilai b = 4 kedalam persamaan 1 untuk mencari nilai a.
36 = 4a + 6b
36 = 4a + 6(4)
12 = 4a
a = 12/4
a = 3
Jadi nilai a = 3 dan beda = 4.
Semoga bermanfaat.



