Rumus dan Contoh Soal Persamaan Lingkaran

Pada artikel ini kita akan belajar mengenai Materi Pengertian, Rumus, dan Bagaimana Cara Menghitung Persamaan Lingkaran dengan Contoh Soal yang mudah dipahami

tugassains.com – Persamaan Lingkaran adalah persamaan matematika dengan dua variabel yang memiliki bentuk lingkaran pada kordinat kartesius.

Dengan Persamaan Lingkaran kita dapat menggambar sebuah lingkaran dengan perhitungan yang presisi pada bidang kordinat kartesius.

Dan sebaliknya pada bentuk lingkaran di bidang kartesius dapat kita hitung persamaan lingkaran menggunakan Rumus Persamaan Lingkaran berikut.

Rumus dan Contoh Soal Persamaan Lingkaran

Rumus Persamaan Lingkaran

Rumus Persamaan Lingkaran pada titik pusat O(0,0) dan jari-jari r

Sebuah lingkaran dalam bidang koordinat kartesius dengan titik pusat O(0,0) dan jari-jari r dapat menggunakan rumus berikut:

Rumus Persamaan Lingkaran pada titik pusat O(0,0) dan jari-jari r

Rumus Persamaan Lingkaran pada titik pusat P(a,b) dan jari-jari r

Untuk mencari persamaan lingkaran pada titik pusat P(a,b) dan jari-jari r pada bidang kordinat kartesius dapat menggunakan persamaan berikut:

Rumus Persamaan Lingkaran pada titik pusat P(a,b) dan jari-jari r

Dari rumus tersebut kita dapat mencari perssamaan lingkaran yang memiliki titik pusat di sembarang titik pada bidang koordinat kartesius.

Sedangkan untuk mencari titik pusat dan jari-jari r dari persamaan lingkaran yang bertitik pusat P(a,b) kita dapat menghitung menggunakan rumus berikut:

Rumus Titik Pusat dan Jari-jari dari Persamaan Lingkaran

Baca juga: Pengertian, Rumus dan Cara Menghitung Tembereng Lingkaran

Untuk memahami lebih lanjut dari Rumus Persamaan Lingkaran kita dapat melatih dengan Contoh Soal Pembahasan Persamaan Lingkaran berikut.

Contoh Soal Persamaan Lingkaran

1. Carilah persamaan lingkaran yang memiliki titik pusat O(0,0) dan memiliki jari-jari r sepanjang 5!

Jawab: Untuk mencari persamaan lingkaran yang memiliki titik pusat O(0,0) kita dapat menggunakan rumus persamaan lingkaran:

titik pusat O(0,0) dan r = 5

Diperoleh persamaan Lingkaran x² + y² = 25.

2. Carilah persamaan lingkaran dari gambar lingkaran di bidang kartesius berikut.

Jawab:
diketahui:

• titik pusat = O(0,0)
• jari-jari r = 3

Penyelesaian: Untuk mencari persamaan lingkaran kita dapat mensubtitusikan nilai jari-jari dan titik pusat kedalam rumus persamaan lingkaran.

Jadi diperoleh persamaan lingkaran x² + y² = 9.

3. Tentukan panjang jari-jari dari persamaan lingkaran x² + y² = 48!

Jawab: Panjang jari jari dapat di cari dengan menggunakan rumus dasar persamaan lingkaran seperti berikut.

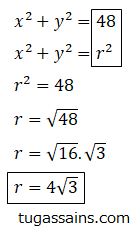
Jadi panjang jari-jari lingkaran tersebut 4√3.

4. Sebuah lingkaran dibidang kartesius memiliki titik pusat P(8,-3) dan jari-jari sebesar 9. Carilah persamaan lingkarannya!

Jawab:
diketahui:

• P(a,b) = P(8,-3)
• r = 9

Penyelesaian: Persamaan lingkaran dapat diperoleh dengan mencari menggunakan rumus persamaan lingkaran pada titik pusat P(a,b).

Jadi diperoleh persamaan lingkaran x² + y² – 16x + 6y – 8 = 0.

5. Carilah persamaan lingkaran dari lingkaran pada kordinat kartesius berikut.

Jawab:
diketahui:

• P(a,b) = P(5,4)
• r = (5 – 1)
• r = 4

Penyelesaian: Cari persamaan lingkaran dengan mensubtitusikan titik pusat dan panjang jari-jari kedalam rumus mencari persamaan lingkaran.

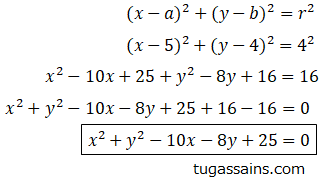
Jadi diperoleh persamaan lingkaran x² + y² – 10x – 8y + 25 = 0.

6. Carilah titik pusat dari persamaan lingkaran x² + y² – 16x – 18y + 33 = 0 beserta panjang jari-jari lingkaran tersebut!

Jawab:
diketahui:

• x² + y² – 8x – 18y + 33 = 0
• x² + y² + Ax + By + C = 0
• sehingga: A = -8
• B = -18
• C = 33

Penyelesaian: Cari titik pusat dari persamaan lingkaran menggunakan rumus.

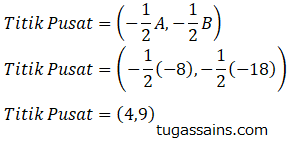
Kemudian cari panjang jari-jari dari persamaan lingkaran dengan menghitung menggunakan rumus.

Jadi titik pusat lingkaran P(4,9) dan jari-jari lingkaran 8.

7. Carilah Panjang diameter dan titik pusat dari persamaan lingkaran x² + y² + 6x – 10y – 15 = 0 tersebut!

Jawab:
diketahui:

• x² + y² + 6x – 10y – 15 = 0
• x² + y² + Ax + By + C = 0
• sehingga: A = 6
• B = -10
• C = -15

Penyelesaian: Cari titik pusat dari persamaan lingkaran menggunakan rumus titik pusat persamaan lingkaran.

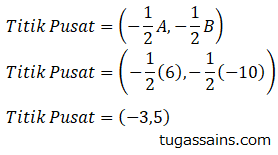
Kemudian cari panjang jari-jari lingkaran dari persamaan lingkaran.

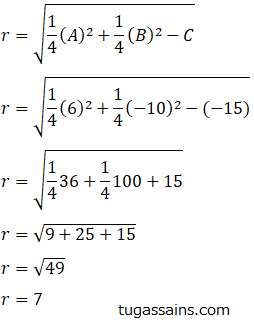
Cari panjang diameter yaitu panjang diameter sama dengan dua kali panjang jari-jari.

• d = 2r
• d = 2(7)
• d = 14

Jadi titik pusat lingkaran P(-3,5) dan diameter lingkaran 14.

Baca juga: Pengertian, Rumus dan Cara Menghitung Juring Lingkaran

Jangan lupa bagikan jika ada yang ingin ditanyakan silahkan bertanya melalui kolom komentar dibawah, terima kasih semoga bermanfaat.