Rumus dan Contoh Soal Permutasi

tugassains.com – Ketika belajar Matematika berkaitan dengan Peluang atau Probabilitas kita akan mempelajari Permutasi sebagai perhitungannya.

Yang mana Permutasi berbeda dengan Kombinasi meskipun sama-sama digunakan ketika menghitung pada Kaidah Pencacahan di dalam Matematika dan menggunakan Faktorial.

Berikut merupakan pembahasan mengenai Pengertian Permutasi, Rumus Permutasi, Penggunaan Permutasi dan Contoh Soal Permutasi yang dibahas secara lengkap dan mudah.

Rumus dan Contoh Soal Permutasi

Baca Juga

Pengertian Permutasi

Permutasi adalah penyusunan kembali objek-objek dengan susunan urutan yang berbeda dari sebelumnya biasanya digunakan dalam menghitung peluang atau probabilitas.

Permutasi didalam matematika di lambangkan dengan huruf P. Sehingga ketika kita dalam menghitung peluang atau kaidah pencacahan akan menuliskan permutasi disimbolkan dengan P yang berarti Permutasi.

Permutasi sendiri digunakan berdasarkan penyusunan objek-objek yang memperhatikan urutan.

Rumus Permutasi

Permutasi r dari n unsur berbeda (dengan syarat r ≤ n) yang mana banyak susunan berbeda dari r unsur yang diambil dari n unsur berbeda dengan syarat memperhatikan urutan atau posisi.

• Permutasi r unsur dari n di notasikan dengan _nP_r,
• P(n,r), P_rⁿ atau P_n,r dan memiliki
• Rumus Permutasi sebagai berikut:

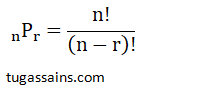
dengan syarat bahwa r ≤ n serta r dan n bilangan bulat. Jika kita menemui besar r = n maka permutasi _nP_r = n!. 

Untuk Cara mudah notasi permutasi dapat kita ucapkan dengan NPR, yang mana posisi n lebih dahulu atau diatas dari r.

Rumus Permutasi Beberapa Unsur yang Sama

Selain permutasi dari n unsur yang berbeda, terdapat permutasi dari beberapa unsur yang sama misalnya seperti permutasi susunan huruf atau kata.

Permutasi dari n unsur yang memuat k₁ unsur yang sama dari jenis ke-1, k₂ unsur yang sama dari jenis ke-2, … k₅ unsur yang sama dari jenis ke-r (k₁ + k₂ + … + r ≤ n). Memiliki rumus Permutasi dengan beberapa unsur yang sama sebagai berikut:

Dengan syarat n dan r bilangan asli.

Rumus Permutasi Siklis

Permutasi Siklis dimana permutasi yang memiliki susunan berurutan membentuk sebuah lingkaran. Misalnya adalah permutasi siklis dari A – B – C berikut.

Permutasi Siklis

Permutasi siklis dari n unsur memiliki rumus yang mudah yaitu:

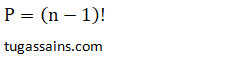
Dengan syarat n adalah bilangan asli.

Penggunaan Permutasi

Kapan Permutasi digunakan? Permutasi digunakan saat kita menemui beberapa hal berikut:

• Urutan atau posisi diperhatikan.
• Pada posisi jabatan, susunan angka dan huruf
• Posisi juara di sebuah perlombaan

Sehingga ketika kita akan menghitung menemukan salah satu dari 3 hal tersebut, Kaidah Permutasi digunakan.

Setelah belajar mengenai Rumus dan Penggunaan Permutasi mari kita latih diri melalui latihan contoh soal permutasi berikut.

Contoh Soal Permutasi

1. Sebuah kelas akan melaksanakan pemilihan pengurus kelas yang terdiri dari ketua kelas, wakil ketua kelas, dan sekretaris kelas. Jika jabatan tidak boleh dirangkap, tentukan banyak kemungkinan susunan pengurus kelas yang terbentuk jika banyak siswa terdapat 36!

Jawab:
diketahui:

• n = 36 (banyak siswa)
• r = 3 (jabatan pengurus)

ditanya: Banyak kemungkinan susunan pengurus?

Penyelesaian: Sistem pemilihan pengurus kelas tersebut memperhatikan posisi sehingga kita dapat mencari banyak kemungkinan susunan penguruss kelas dengan menggunakan Rumus Permutasi.

Jadi banyak kemungkinan susunan yang terbentuk sebanyak 42.840 .

2. Suatu perlombaan puisi diikuti oleh 24 orang peserta yang mana 12 dari keseluruhan peserta gagal disaat penyisihan, jika perlombaan puisi tersebut terdapat juara 1, juara 2 dan tiga juara harapan. Tentukan banyak kemungkinan posisi juara yang terbentuk.

Jawab:
diketahui:

• jumlah peserta = 24
• gagal dalam penyisihan = 12
• n = 24 – 12
• n = 12 (sisa peserta)
• r = 4 (posisi juara)

ditanya: Banyak kemungkinan posisi juara yang terbentuk?

Penyelesaian: Pada soal tersebut memperhatikan posisi juara, sehingga dapat diselesaikan dengan permutasi.

Jadi kemungkinan posisi juara yang terbentuk sebanyak 11.880 .

3. Berapa banyak kata atau susunan huruf yang dapat dibentuk dengan kata “KATAK”?

Jawab: Susunan kata yang dapat disusun dari kata “KATAK” adalah jenis permutasi dengan beberapa unsur yang sama.

diketahui: KATAK

• Jumlah huruf = 5
• huruf K = p = 2
• huruf A = q = 2
• huruf T  = r = 1

ditanya: Banyak kata atau susunan huruf yang dapat dibentuk?

Penyelesaian: Banyak kata yang dapat dibentuk dapat kita cari dengan menggunakan rumus permutasi dengan beberapa unsur yang sama.

Jadi banyak kata yang dapat yang disusun yaitu 30.

4. Carilah banyak susunan kata yang dapat dibentuk dari “MANAJEMEN”?

Jawab: Banyak susunan kata yang dapat dibentuk merupakan jenis permutasi dengan beberapa unsur yang sama.

diketahui: MANAJEMEN

• Jumlah huruf = 9
• huruf M = p = 2
• huruf A = q = 2
• huruf N = r = 2
• huruf J = s = 1
• huruf E = t = 2

ditanya: Banyak kata atau susunan huruf yang dapat dibentuk?

Penyelesaian: Jadi banyak kata yang dapat dibentuk dapat kita cari dengan menggunakan rumus permutasi.

Jadi susunan kata yang dapat dibentuk sebanyak 22.680 .

5. Ada 5 orang anak yang akan melakukan permainan tradisional, dimana permainan tersebut dilakukan dengan duduk melingkar. Berapa banyak posisi susunan duduk yang dapat dibentuk oleh 5 orang tersebut?

Jawab: Untuk mencari banyak cara duduk melingkar, hal tersebut merupakan bagian dari permutasi siklis. 

diketahui: n = 5

ditanya: Banyak posisi duduk yang dapat dibentuk?

Jawab: Banyak posisi duduk melingkar dapat kita cari dengan menggunakan rumus permutasi siklis.

• P = (n – 1)!
• P = (5 – 1)!
• P = 4!
• P = 4 × 3 × 2 × 1
• P = 24

Jadi banyak cara posisi duduk melingkar yaitu 24 cara.

6. Petinggi sebuah Perusahaan Tekstil 7 orang masing-masing Direktur, Wakil Direktur, Penanggung Jawab, Manager Produksi, Investor dan dua Sekretaris. Jika Direktur dan Wakil Direktur harus duduk bersebelahan. Tentukan banyak cara posisi duduk di meja bundar rapat?

Jawab: Pada soal tersebut merupakan permutasi siklis namun perlu diperhatikan bahwa posisi duduk Direktur dan Wakil Direktur menjadi dua permutasi. Sehingga banyak peserta dapat dianggap menjadi 6 peserta rapat.

• P = (n – 1) × 2! →posisi duduk Direktur dan Wakil Direktur
• P = (6 – 1)! × 2!
• P = (5)! × 2!
• P = 5 × 4 × 3 × 2 × 1 × 2 × 1
• P = 240 posisi duduk

Jadi banyak posisi duduk dalam rapat yaitu 240 posisi.

Baca Juga Pengertian dan Contoh Soal Faktorial

Jika ada yang ingin ditanyakan terkait materi Rumus dan Contoh Soal Permutasi dapat kalian tanyakan melalui kolom komentar.

Jangan lupa bagikan terima kasih, Semoga bermanfaat.