tugassains.com – Matriks adalah materi matematika yang berisi mengenai kumpulan angka baik konstanta maupun variabel yang disusun berdasarkan elemen kolom dan elemen baris dalam suatu tanda kurung siku.
Didalam matriks terdapat jenis Matriks Singular dan Matriks Nonsingular dimana jenis tersebut diperoleh dari perhitungan determinan dari komponen matriks.
- Matriks Singular adalah matriks yang memiliki nilai determinan |A| = 0
- Matriks Nonsingular adalah matriks yang memiliki nilai determinan |A| ≠ 0
Determinan adalah nilai yang diperoleh dari sebuah matriks bujur sangkar dengan cara sedemikian rupa.
Perlu dicatat bahwa determinan hanya terdapat pada matriks persegi artinya Matriks Singular dan Matriks Nonsingular merupakan matriks persegi.
Baca Juga Cara Menghitung Determinan Matriks 2×2
Rumus Matriks Singular
Untuk dapat menentukan matriks singular baik itu membuktikan matriks singular atau mencari nilai variabel pada matriks singular dapat kita gunakan rumus dan langkah berikut:
1. Buktikan bahwa matriks A adalah Matriks Singular:

Jawab: Cari nilai determinan untuk mencari pembuktian matriks singular yaitu singular jika |A| = 0.

Karena determinan bernilai sama dengan nol sehingga matriks A adalah matriks singular.
2. Carilah nilai x agar matriks B singular:
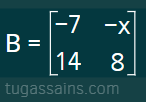
Jawab: Dengan menggunakan determinan dan menyelesaikan persamaan determinan kita dapat memperoleh nilai x dari matriks.

Agar matriks Y singular nilai x harus bernilai 4.
Untuk melatih pemahaman mengenai Matriks Singular mari kita coba pelajari Contoh Soal Matriks Singular yang telah disertai Pembahasan.
Contoh Soal Matriks Singular
1. Buktikanlah bahwa matriks A berikut termasuk Matriks Singular!

Jawab: Untuk membuktikan apakah matriks tersebut singular dapat kita tentukan dengan mencari nilai determinannya.

Karena nilai determinan matriks A sama dengan nol maka matriks A singular.
2. Dari matriks B berordo 2×2 tentukan apakah Matriks B termasuk dalam matriks singular?

Jawab:

Karena nilai determinan bernilai tidak sama dengan nol maka Matriks B tidak Singular.
3. Buktikan bahwa matriks K berordo 3×3 tersebut Matriks Singular!

Jawab: Hitung nilai determinan matriks 3×3 dan buktikan jika memiliki nilai determinan 0.
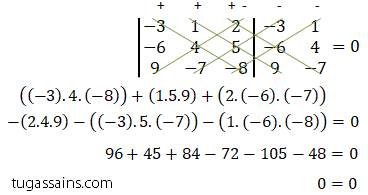
Jadi matriks K 3×3 tersebut merupakan matriks singular.
4. Carilah nilai dari x dari Matriks L Singular berordo 2×2 berikut!

Jawab: Karena Matriks L adalah matriks singular sehingga nilai |L| = 0, kemudian hitung nilai determinan untuk mencari nilai x pada Matriks L.
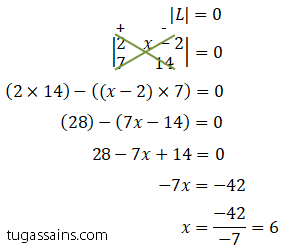
Jadi nilai x pada Matriks L singular bernilai x = 6.
5. Jika Matriks M berordo 2×2 adalah matriks singular, Tentukan nilai y dari matriks.

Jawab: Nilai y dari Matriks M berordo 2×2 yang singular dapat dicari dengan menghitung nilai determinan M, karena Matriks M singular sehingga |M| = 0.
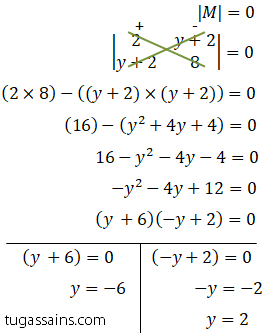
Jadi nilai y dari matriks M singular bernilai y = -6 atau y = 2.
6. Sebuah Matriks N berordo 3×3 carilah nilai x agar matriks singular.

Jawab: Agar matriks N singular maka nilai dari determinan |N| = 0, sehingga akan diperoleh nilai x dari matriks N.

Jadi nilai x pada Matriks N agar singular bernilai -24.
Baca Juga Cara Menghitung Determinan Matriks 3×3
Semoga bermanfaat jangan lupa bagikan dan jika ada yang ingin ditanyakan silahkan bertanya di kolom komentar terima kasih.




