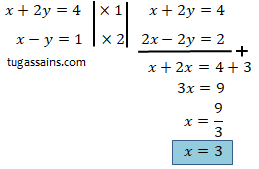Mengenal Sistem Persamaan Linear Dua Variabel

tugassains.com – Sistem Persamaan Linear Dua Variabel (SPLDV) merupakan salah satu materi yang kita temukan ketika mempelajari Matematika.

Melalui artikel ini kita dapat belajar memahami Persamaan Linear Dua Variabel mulai dari Pengertian, Ciri-ciri, Rumus Penyelesaian dan Contoh Soal Penyelesaian.

Mengenal Sistem Persamaan Linear Dua Variabel

Pengertian Persamaan Linear Dua Variabel

Apa itu persamaan linear dua variabel? Persaman Linear Dua Variabel adalah persamaan linear matematika yang memiliki dua buah variabel, dengan masing-masing variabel memiliki nilai yang pasti.

Persamaan Linear Dua Variabel

Dimana variabel tersebut dapat dimisalkan dengan x dan y kemudian dapat dicari nilai variabel tersebut dengan berbagai Metode Rumus Persamaan Linear Variabel

Ciri-ciri Persamaan Linear Dua Variabel

Adapun ciri-ciri dari persamaan linear dua variabel yaitu sebagai berikut:

• Persamaan dihubungkan oleh tanda sama dengan (=).
• Tidak terdapat perkalian antar variabel.
• Masing-masing variabel memiliki pangkat satu.
• Masing-masing variabel memiliki nilai yang pasti (tidak kurang dan lebih).

Setelah tahu mengenai ciri-ciri dari persamaan linear dua variabel mari kita belajar rumus persamaan linear dua variabel berikut.

Rumus Persamaan Linear Dua Variabel

Untuk dapat menyelesaikan sebuah Sistem Persamaan Linear Dua Variabel terdapat empat buah Rumus Persamaan Linear Dua Variabel berikut:

1. Metode Subtitusi
2. Metode Eliminasi
3. Metode Gabungan(Subtitusi dan Eliminasi)
4. Metode Grafik

Yang mana pada masing-masing metode penyelesaian memiliki cara penyelesaian yang berbeda-beda, namun tetap memiliki hasil penyelesaian yang sama.

Metode Subtitusi

Metode Subtitusi persamaan linear dua variabel adalah salah satu cara penyelesaian yang menggunakan pensubtitusian variabel ke dalam persamaan hingga diketahui nilai variabelnya.

Langkah-langkah Metode Subtitusi:

diketahui:

• x + 2y = 4 …(1)
• x – y = 1 …(2)

1. Cari persamaan linear yang sederhana agar dapat diubah menjadi bentuk x =  atau y = agar dapat disubtitusikan.
   

   Ubah persamaan 2 menjadi x =x – y = 1
    x = 1
   + y   …(3)

2. Kemudian lakukan subtitusikan persamaan satu ke dalam persamaan lain untuk mencari nilai salah satu variabel. Subtitusi persamaan 3 ke dalam persamaan 1
        
   x + 2y = 4
   (1 + y) + 2y = 4   (melakukan subtitusi)
            1 + 3y = 4
                3y = 3
                y = 1
   

   Sehingga diketahui nilai variabel y = 1

3. Setelah diketahui nilai salah satu variabel subtitusikan ke dalam salah satu persamaan untuk mencari nilai variabel lain. Subtitusi nilai y = 1 ke persamaan 1
   x + 2y = 4
   x + 2(1) = 4
   x + 2 = 4
   x = 2
   Jadi diperoleh nilai x = 2

Sehingga diperoleh nilai x = 2 dan y = 1.

Baca Juga Cara Menyelesaikan SPLDV Metode Substitusi

Metode Eliminasi

Metode eliminasi adalah salah satu metode penyelesaian persamaan linear yang dilakukan dengan mengeleminasi variabel nya hingga menemukan penyelesaian.

Langkah-langkah Metode Eliminasi:

diketahui:
x + 2y = 4 …(1)
x – y = 1 …(2)

1. Langkah pertama dilakukan dengan mengeleminasi salah satu variabel misalkan variabel x untuk mencari nilai variabel y.
   

   Eliminasi x dengan mengurangkan variabel x, (jika koefisien variabel berbeda samakan dengan mengalikan sembarang bilangan agar kedua koefisien di dua persamaan bernilai sama).

   Baca Juga :

   Cara Menyelesaikan SPLDV Metode Campuran
   
   
   
   

1. Kemudian eliminasi variabel yang sudah diketahui nilainya untuk mencari nilai variabel yang belum diketahui. Eliminasi variabel y dengan menyamakan koefisien menjadi dua (kalikan persamaan 2 dengan 2).
   

Sehingga diperoleh nilai variabel  x = 2 dan y = 1

Baca Juga Cara Menyelesaikan SPLDV Metode Eliminasi

Metode Gabungan

Metode Gabungan merupakan salah satu penyelesaian persamaan linear dua variabel dengan menggunakan gabungan metode Eliminasi dan Subtitusi.

Pada metode gabungan yang biasa dilakukan yaitu dengan melakukan metode eliminasi terlebih dahulu kemudian menggunakan metode subtitusi setelahnya.

Langkah-langkah metode gabungan:

diketahui:
x + 2y = 4    …(1)
x – y = 1    …(2)

1. Langkah pertama lakukan eliminasi terlebih dahulu pada persamaan yang sederhana.
   

   Eliminasi x dari persamaan 1 dan 2 untuk mencari nilai y dari persamaan.

   
   

1. Setelah diperoleh nilai salah satu persamaan, lakukan subtitusi ke dalam persamaan untuk mencari nilai variabel lain. Subtitusi nilai y = 1 kedalam persamaan 2 untuk mencari nilai y.

   x – y = 1
   x – 1 = 1
   x = 1 + 1
   x = 2

Jadi diperoleh penyelesaian x = 2 dan y = 1

Metode Grafik

Penyelesaian persamaan linear dua variabel dapat diselesaikan dengan menggambarkan lalu mancari penyelesaian melalui titik potong pada grafik.

diketahui:
x + 2y = 4 …(1)
x – y = 1 …(2)

Langkah-langkah Metode Grafik

1. Gambar bentuk grafik masing-masing persamaan dengan bantuan memisalkan (misal jika x bernilai 0 maka grafik akan melalui sumbu y pada koordinat).
   

   Pada persamaan 1 memotong sumbu x dan y pada:

   
   

   Pada persamaan 2 memotong sumbu x dan y pada

   
   

1. Gambarkan kedua grafik pada bidang kartesius setelah diketahui titik koordinatnya. Cari disebelah mana grafik kedua persamaan berpotongan. 
   

   Maka dapat diketahui dari letak perpotongan kedua grafik pada koordinat
   (2, 1) sehingga x = 2 dan y = 1.

Selain itu terdapat cara untuk menyelesaikan Persamaan Linear Dua Variabel secara cepat dan benar terutama ketika ujian dapat kita gunakan Cara Cepat Menyelesaikan SPLDV.

Setelah mengetahui Rumus Persamaan Linear Dua Variabel mari kita belajar melalui Contoh Soal Pembahasan yang mudah dipahami berikut.

Contoh Menyelesaikan Persamaan Linear Dua Variabel

Setelah mengetahui mengenai metode-metode penyelesaian mari kita latih dengan Contoh Soal Penyelesaian berikut

Menggunakan Metode Subtitusi

Selesaikan persamaan linear dua variabel berikut menggunakan metode subtitusi.

 x + y = 5 … (1)
3x – y = 3 … (2)

Penyelesaian: Selesaikan dengan metode subtitusi yaitu ubah dalam bentuk x =  dari persamaan 1.

x + y = 5 
x = 5 – y … (3)

Subtitusi persamaan 3 kedalam persamaan 2.

3x – y = 3
3(5 – y) – y = 3
15 – 3y – y = 3
15 – 4y = 3
-4y = -12
y = -12/-4
y = 3

Diperoleh nilai y = 3, subtitusikan nilai y ke dalam persamaan 1 untuk mencari nilai x.

x + y = 5
x + 3 = 5
x = 5 – 3 
x = 2

Jadi persamaan linear dua variabel tersebut memiliki penyelesaian x = 2 dan y = 3

Menggunakan Metode Eliminasi

Selesaikan Contoh Soal Cerita SPLDV berikut menggunakan metode eliminasi dengan benar.

Diketahui Budi membeli 3 buku dan 2 pena seharga Rp. 11.000 kemudian Rudi membeli 2 buku dan 2 pena seharga Rp. 8.000. Tentukan harga buku dan pena tersebut.

Untuk menyelesaikan Contoh Soal Cerita Persamaan Linear Dua Variabel tersebut mari kita misalkan kedalam bentuk persamaan.

Misalkan: buku = x dan pena = y.
3x + 2y = 11.000 …(1)
2x + 2y =   8.000 …(2)

Selesaikan persamaan menggunakan metode eliminasi, eliminasi y dari persamaan 1 dan 2 untuk mencari nilai y.

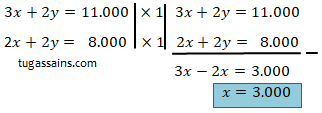
Setelah diketahui nilai x, eliminasi x dari persamaan 1 dan 2 untuk mencari nilai y.

Sehingga diketahui nilai x atau harga buku Rp. 3.000 dan nilai y atau harga Pena Rp. 2.000.

Menggunakan Metode Gabungan

Cari bilangan penyelesaian masing-masing variabel pada persamaan linear dua variabel menggunakan metode Gabungan.

3x + 5y = 18 …(1)
3x – 2y = -3 …(2)

Eliminasi x dari persamaan 1 dan 2 untuk mencari nilai y dari persamaan

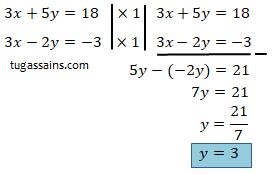
Hitung nilai y = 3 dengan subtitusi nilai x ke dalam persamaan 1.

3x + 5y = 18
3x + 5(3) = 18
3x + 15 = 18
3x = 3
x = 1

Sehingga diperoleh penyelesaian nilai x = 1 dan y = 3.

Menggunakan Metode Grafik

Selesaikan persamaan linear berikut ini menggunakan metode grafik.

x + y = 2 …(1)
 x – y = 4 …(2)

Penyelesaian: Cari koordinat perpotongan sumbu x dan y dari persamaan 1 dan 2 untuk dapat menggambarkan grafik.

Pada persamaan 1 memotong sumbu x dan y pada kordinat

Pada persamaan 2 memotong sumbu x dan y pada kordinat

Setelah itu gambarkan pada bidang koordinat kedua persamaan, kemudian cari titik potong kedua grafik tersebut.

Jadi penyelesaian persamaan linear tersebut pada koordinat bernilai x = 2 dan y = -1.

Bila dirasa masih kurang terhadap contoh soal tersebut anda dapat membaca pada artikel Contoh Soal Persamaan Linear Dua Variabel sebagai bahan belajar lebih lanjut.

Jika ada yang ingin ditanyakan terkait materi Mengenal Sistem Persamaan Linear Dua Variabel dapat kalian tanyakan melalui kolom komentar.

Jangan lupa bagikan terima kasih, Semoga bermanfaat.