tugassains.com – Persamaan Linear Dua Variabel merupakan persamaan linear Matematika yang memiliki dua buah variabel dengan nilai yang pasti.
Yang mana persamaan linear dua variabel dapat dicari dengan beberapa metode
yang mudah yaitu
- Metode Subtitusi
- Metode Eliminasi
- Metode Campuran, dan
- Metode Grafik.
Melalui artikel ini kita dapat belajar menyelesaikan persamaan linear dua variabel dengan menggunakan Metode Grafik yang disertai dengan Contoh Soal Pembahasan
Cara SPLDV Metode Grafik
Metode Grafik merupakan satu dari beberapa metode penyelesaian persamaan linear yang mana diselesaikan dengan bantuan grafik pada bidang koordinat kartesius.
Dimana penyelesaian persamaan linear dua variabel pada Metode Grafik diselesaikan dengan dua langkah yang mudah.
Mencari titik potong x dan y dari masing-masing persamaan untuk dapat menggambarkan grafik pada bidang kordinat kartesius.
Kemudian grafik digambarkan dibidang kartesius dan cari titik potong antara kedua grafik pada bidang kartesius, titik koordinat perpotongan merupakan penyelesaian dari persamaaan.
Mari kita coba menyelesaikan persamaan linear dua variabel berikut selesaikan dengan menggunakan Metode Grafik.
2x – y = 2 …(1)
x + y = 4 …(2)
Untuk menyelesaikan SPLDV (sistem persamaan linear dua variabel) dapat kita selesaikan dengan mengikuti langkah-langkah berikut.
Langkah Pertama
Cari bentuk grafik dari kedua persamaan linear dengan bantuan memisalkan misal x bernilai nol maka y bernilai begitu juga untuk mencari nilai x untuk memperoleh koordinat persamaan.
Mencari bentuk grafik pada persamaan 1 dengan memisalkan x bernilai nol dan y bernilai nol untuk mencari titik koordinat masing-masing persamaan.
jika x = 0 maka grafik memotong sumbu y pada titik:

jika y = 0 maka grafik memotong sumbu x pada titik:

Persamaan 1 melalui titik (0, -2) dan titik (1, 0).
Mencari bentuk grafik pada persamaan 2 dengan memisalkan x bernilai nol dan y bernilai nol untuk mencari titik koordinat masing-masing persamaan.
jika x = 0 maka grafik memotong sumbu y pada titik:

jika y = 0 maka grafik memotong sumbu x pada titik:

Persamaan 2 melalui titik (0, 4) dan titik (4, 0).
Langkah Kedua
Gambarkan grafik sesuai dengan titik koordinat yang dicari pada bidang koordinat kartesius, Penyelesaian dapat dicari pada perpotongan grafik kedua persamaan.

Kedua grafik memotong pada koordinat (2, 2) sehingga diperoleh penyelesain x = 2 dan y = 2.
Setelah mengetahui cara penyelesaian Metode Grafik dapat kita latih pemahaman kita lebih lanjut menggunakan Contoh Soal Pembahasan SPLDV Metode Grafik berikut.
Contoh Soal SPLDV Metode Grafik
1. Selesaikan persamaan linear dua variabel berikut menggunakan Metode Grafik!
x + y = -2 …(1)
x – y = 4 …(2)
Penyelesaian: Cari titik potong grafik pada sumbu x dan y dari persamaan 1 dan 2.
Persamaan 1 jika x = 0 maka grafik memotong sumbu y pada titik:

jika y = 0 maka grafik memotong sumbu x pada titik:
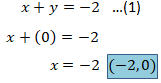
Persamaan 1 melalui titik (0, -2) dan titik (-2, 0).
Persamaan 2 jika x = 0 maka grafik memotong sumbu y pada titik:
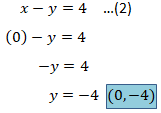
jika y = 0 maka grafik memotong sumbu x pada titik:
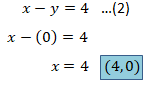
Persamaan 2 melalui titik (0, -4) dan titik (4, 0).
Cari titik potong kedua grafik pada bidang kordinat kartesius untuk mengetahui penyelesaian dari persamaan linear dua variabel tersebut.
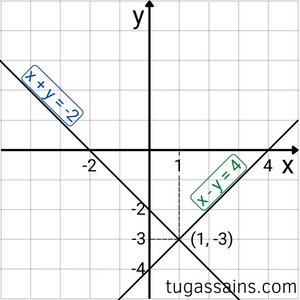
Jadi penyelesaian persamaan bernilai x = -3 dan y = 1.
2. Hitung nilai variabel x dan y dari persamaan linear dua variabel menggunakan Metode Grafik.
x – 2y = -4 …(1)
x + y = -1
…(2)
Penyelesaian: Cari titik potong bidang koordinat pada sumbu x dan y dari persamaan 1 dan persamaan 2 pada bidang kordinat kartesius.
Persamaan 1 jika x = 0 maka grafik memotong sumbu y pada titik:

jika y = 0 maka grafik memotong sumbu x pada titik:

Persamaan 1 melalui titik (0, 2) dan titik (-2, 0).
Persamaan 2 jika x = 0 maka grafik memotong sumbu y pada titik:

jika y = 0 maka grafik memotong sumbu x pada titik:

Persamaan 2 melalui titik (0, -1) dan titik (-1, 0).
Gambarkan grafik kedua persamaan pada bidang kordinat dan cari titik potong kedua grafik sebagai penyelesaian persamaan linear dua variabel tersebut.

Jadi nilai variabel x = -2 dan y = 1.
Jika ada yang ingin ditanyakan terkait materi Cara Menyelesaikan SPLDV Metode Campuran dapat kalian tanyakan melalui kolom komentar.
Jangan lupa bagikan terima kasih, Semoga bermanfaat.


