tugassains.com – Persamaan Linear Dua Variabel merupakan persamaan linear dalam Matematika yang memiliki dua buah variabel dengan nilai yang pasti.
Untuk dapat menyelesaikan Sistem Persamaan Linear Dua Variabel terdapat beberapa cara yaitu dengan
Metode Eliminasi, Metode Subtitusi, Metode Campuran dan Metode Grafik.
Melalui artikel ini kita akan belajar mengenai Penyelesaian Persamaan Linear Dua Variabel dengan menggunakan Metode Campuran yang disertai dengan Contoh Soal Pembahasan.
 |
| Cara Menyelesaikan SPLDV Metode Campuran |
Cara SPLDV Metode Campuran
Metode Campuran untuk menyelesaikan SPLDV merupakan Metode Gabungan dari Metode Eliminasi dan Metode Subtitusi, yang mana metode ini banyak digunakan untuk menyelesaikan SPLDV.
 |
| Langkah Penyelesaian SPLDV Metode Campuran |
Untuk dapat menyelesaikan SPLDV menggunakan Metode Campuran dapat kita lakukan dengan mengeliminasi salah satu variabel untuk dapat mengetahui nilai variabel lain.
Kemudian mensubtitusikan ke dalam persamaan nilai variabel yang diketahui untuk menghitung nilai variabel lain, lebih mudahnya mari kita ikuti langkah langkah berikut.
Diketahui persamaan linear dua variabel berikut, hitunglah nilai variabel x dan y dari persamaan.
- x + 3y = 8 …(1)
- x – 2y = -7 …(2)
Langkah pertama: Eliminasi salah satu variabel yang paling sederhana dari persamaan linear dua variabel tersebut.
Eliminasi x dari persamaan 1 dan 2 untuk mencari nilai y.
Langkah kedua: Setelah nilai y diketahui subtitusikan nilai x kedalam salah satu persamaan untuk mencari nilai x.
Subtitusi y = 3 kedalam persamaan 1 untuk mencari nilai x.
- x + 3y = 8
- x + 3(3) = 8
- x + 9 = 8
- x = 8 – 9
- x = -1
Sehingga diketahui nilai variabel pada SPLDV tersebut yaitu x = -1 dan y = 3.
Untuk lebih lanjut memahami Cara Menyelesaiakan SPLDV Metode Campuran dapat kita latih dengan Contoh Soal Pembahasan SPLDV Metode Campuran berikut.
Contoh Soal SPLDV Metode Campuran
1. Hitunglah nilai variabel x dan y dari persamaan linear dua variabel berikut ini.
- x – y = 8 …(1)
- x + 2y = 20 …(2)
Penyelesaian: Untuk menyelesaikan dari SPLDV tersebut menggunakan metode campuran, mari kita eliminasi terlebih dahulu variabel yang sederhana dari kedua persamaan tersebut.
Eliminasi x dari persamaan 1 dan 2 untuk mencari nilai y.
Subtitusi nilai y = 4 ke persamaan 1 untuk mencari nilai x.
- x – y = 8
- x – 4 = 8
- x = 12
Jadi nilai variabel x = 12 dan y = 3.
2. Budi membeli 3 buah pena dan 5 buah buku seharga 34.000 kemudian Rizky membeli 3 pena dan 6 buah buku seharga 36.000. Tentukan harga sebuah pena dan sebuah buku yang dibeli oleh Budi dan Rizky.
Jawab: Pada soal tersebut merupakan Contoh Soal Cerita SPLDV sehingga untuk menyelesaikannya kita perlu memisalkan dalam bentuk persamaan terlebih dahulu.
Misal: pena = x dan buku = y
3x + 5y = 34.000
…(1)
2x + 6y = 36.000 …(2)
Penyelesaian: Eliminasi variabel x dari persamaan 1 dan 2 untuk mencari nilai variabel y.
Subtitusi nilai y = 5.000 kedalam persamaan 1 untuk mencari nilai x dari persamaan.
Sehingga x atau pena memiliki harga Rp. 3.000 dan y atau buku memiliki harga Rp. 5.000.
3. Carilah bilangan penyelesaian dari SPLDV berikut.
a + 3b = 17 …(1)
5a – 3b = -5
…(2)
Penyelesaian: Eliminasi variabel b dari persamaan 1 dan 2 untuk mencari nilai variabel a.
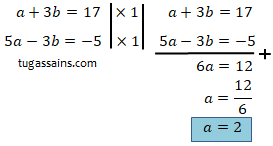
Kemudian lakukan subtitusi nilai variabel a = 2 ke dalam persamaan 1 untuk mencari nilai variabel b.
Jadi bilangan penyelesaian a = 2 dan b = 5.
Jika ada yang ingin ditanyakan terkait materi Cara Menyelesaikan SPLDV Metode Campuran dapat kalian tanyakan melalui kolom komentar.
Jangan lupa bagikan terima kasih, Semoga bermanfaat.