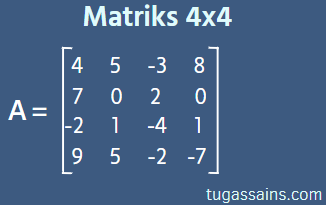
Pada artikel ini kita akan belajar mengenai Bagaimana Cara Menghitung Determinan Matriks ordo 4×4 yang disertai dengan Contoh Soal dan penjelasan yang mudah dipahami
tugassains.com – Matriks merupakan salah satu materi Matematika yang berisikan bilangan konstanta ataupun variabel yang disusun berdasarkan kolom dan baris didalam sebuah tanda kurung.
Dan pada artikel ini kita akan belajar mengenai Pengertian Determinan Matriks, Cara Menghitung Determinan Matriks 4×4, dan Contoh Soal Determinan Matriks 4×4.
Baca Juga Cara Menghitung Determinan Matriks 2×2
Pengertian Determinan Matriks
Determinan matriks adalah suatu bilangan real yang diperoleh dari sebuah matriks bujur sangkar atau matriks persegi dengan suatu proses atau cara tertentu.
Determinan sendiri biasa dinotasikan dengan tanda det(A) atau |A| pada matriks A.
Ingat determinan hanya dapat dihitung pada matriks persegi seperti 2×2, 3×3 dan seterusnya.
Rumus Determinan Matriks 4×4
Untuk dapat menghitung determinan matriks berordo 4×4 kita dapat menggunakan dua buah cara yaitu:
1. Determinan Matriks 4×4 Metode Sarrus
Untuk mencari determinan matriks ordo 4×4 dengan metode sarrus kita memerlukan 4 langkah, berikut adalah langkah penyelesaian dengan penjelasan:
Diketahui: matriks A berordo 4×4

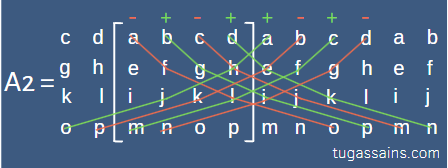
Langkah pertama: Hitung dengan urutan (+ – + – – + – +) dengan jarak 1-1-1

Diperoleh perhitungan:
A1 = afkp – bglm + chin – dejo – ahkn + belo – cfip + dgjm
Langkah kedua: Hitung dengan urutan (- + – + + – + -) dengan jarak 1-2-3
Diperoleh perhitungan:
A2 = -aflo + bgip – chjm + dekn + ahjo – bekp + cflm – dgin
Langkah ketiga: Hitung dengan urutan (+ – + – – + – +) dengan jarak 2-1-2

Diperoleh perhitungan:
A3 = agln – bhio + cejp – dfkm – agjp + bhkm -celn + dfio
Setelah menemukan nilai A1, A2 dan A3 kita dapat langsung menghitung determinan dengan rumus berikut:
Det (A) = A1 + A2 + A3
Selalu perhatikan perhitungan agar tidak terjadi salah hitung.
2. Determinan Matriks 4×4 Metode Kofaktor
Diketahui: matriks A berordo 4×4 carilah nilai determinannya dengan metode kofaktor.

Untuk dapat mencari determinan dengan metode kofaktor kita dapat menghitung dengan 5 langkah berikut, sebelum itu pahami makna di balik angka dibawah komponen matriks:

Langkah pertama: Hitung Minor M11 dan Kofaktor C11 dari a11:

Langkah kedua: Hitung Minor M21 dan Kofaktor C21 dari a21:

Langkah ketiga: Hitung Minor M31 dan Kofaktor C31 dari a31:

Langkah pertama: Hitung Minor M41 dan Kofaktor C41 dari a41:

Langkah kelima:
Hitung nilai determinan dengan rumus berikut:
Det (A) = (a11 × C11) + (a21 ×
C21) + (a31 × C31) +
(a41 × C41)
Lakukan perhitungan secara teliti agar diperoleh hasil perhitungan yang benar.
Contoh Soal Determinan Matriks 4×4
1. Carilah nilai determinan dari matriks berordo 4×4 berikut dengan metode sarrus!

Jawab:
Untuk menghitung determinan dari matriks berordo 4×4 dengan menggunakan metode sarrus dapat kita hitung dengan mencari nilai A1, A2 dan A3 terlebih dahulu.
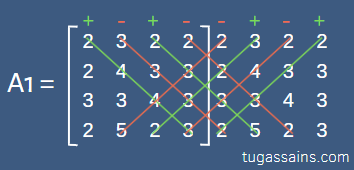
Hitung nilai A1
A1 = (2 × 4 × 4 × 3) – (3 × 3 × 3 × 2) + (2 × 3 × 3 × 5) – (2 × 2 × 3 × 2) – (2 × 3 × 4 × 5) + (3 × 2 × 3 × 2) – (2 × 4 × 3 × 3) + (2 × 3 × 3 × 2)
A1 = 96 – 54 + 90 – 24 – 120 + 36 – 72 + 36
A1 = -12
Kemudian cari nilai A2
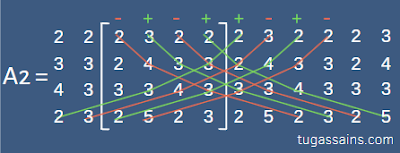
Hitung nilai A2
A2 = -(2 × 4 × 3 × 2) + (3 × 3 × 3 × 3) – (2 × 3 × 3 × 2) + (2 × 2 × 4 × 5) + (2 × 3 × 3 × 2) – (3 × 2 × 4 × 3) + (2 × 4 × 3 × 2) – (2 × 3 × 3 × 5)
A2 = -48 + 81 – 36 + 80 + 36 – 72 + 48 – 90
A2 = -1
Kemudian cari nilai A3

Hitung nilai A3
A3 = (2 × 3 × 3 × 5) – (3 × 3 × 3 × 2) + (2 × 2 × 3 × 3) – (2 × 4 × 4 × 2) – (2 × 3 × 3 × 3) + (3 × 3 × 4 × 2) – (2 × 2 × 3 × 5) + (2 × 4 × 3 × 2)
A3 = 90 – 54 + 36 – 64 – 54 + 72 – 60 + 48
A3 = 14
Kemudian hitung nilai determinan dari matriks 4×4 dengan menjumlahkan nilai A1, A2 dan A3 yang telah diperoleh.
- Det (A) = A1 + A2 + A3
- Det (A) = -12 + (-1) + 14
- Det (A) = 1
Jadi determinan dari matriks A 4×4 tersebut sebesar 1.
2. Gunakan metode kofaktor untuk mencari besar determinan dari matriks A yang berordo 4×4 berikut!

Jawab: Untuk menghitung determinan dengan metode minor kofaktor kita dapat hitung dengan menghitung minor dan kofaktor terlebih dahulu.
Hitung Minor M11 dan Kofaktor C11 dari a11:

a11 = 2
M11 = (4 × 4 × 3) + (3 × 3 × 5) + (3 × 3 × 2) – (3 × 4 × 5) – (4 × 3 × 2) – (3 × 3 × 3)
M11 = 48 + 45 + 18 – 60 – 24 – 27
M11 = 0
C11 = (-1)1+1 × M11
C11 = 1 × 0
C11 = 0
Hitung Minor M21 dan Kofaktor C21 dari a21:
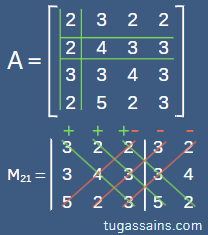
a21 = 2
M21 = (3 × 4 × 3) + (2 × 3 × 5) + (2 × 3 × 2) – (2 × 4 × 5) – (3 × 3 × 2) – (2 × 3 × 3)
M21 = 36 + 30 + 12 – 40 – 18 – 18
M21 = 2
C21 = (-1)2+1 × M21
C21 = -1 × 2
C21 = -2
Hitung Minor M31 dan Kofaktor C31 dari a31:

a31 = 3
M31 = (3 × 3 × 3) + (2 × 3 × 5) + (2 × 4 × 2) – (2 × 3 × 5) – (3 × 3 × 2) – (2 × 4 × 3)
M31 = 27 + 30 + 16 – 30 – 18 – 24
M31 = 1
C31 = (-1)3+1 × M31
C31 = 1 × 1
C31 = 1
Hitung Minor M41 dan Kofaktor C41 dari a41:

a41 = 2
M41 = (3 × 3 × 3) + (2 × 3 × 3) + (2 × 4 × 4) – (2 × 3 × 3) – (3 × 3 × 4) – (2 × 4 × 3)
M41 = 27 + 18 + 32 – 18 – 36 – 24
M41 = -1
C41 = (-1)4+1 × M41
C41 = -1 × -1
C41 = 1
Hitung besar determinan dari matriks tersebut dengan rumus determinan minor kofaktor:
Det (A) = (a11 × C11) + (a21 × C21) + (a31 × C31) + (a41 × C41)
Det (A) = (2 × 0) + (2 × (-2)) + (3 × 1) + (2 × 1)
Det (A) = 0 – 4 + 3+ 2
Det (A) = 1
Jadi besar determinan dari matrik A tersebut sebesar 1.
Baca Juga Cara Menghitung Determinan Matriks 3×3
Semoga bermanfaat jika ada yang ingin ditanyakan silahkan bertanya di kolom komentar dan jangan lupa bagikan.