Pada artikel ini kita akan belajar mengenai Pengertian, Cara Mencari dan Contoh Soal Transpose Matriks yang dijelaskan secara mudah agar dapat dipahami
tugassains.com – Matriks adalah salah satu materi matematika yang berisi baik itu konstanta maupun variabel yang disusun berdasarkan baris dan kolom dalam tanda kurung siku.
Matriks sendiri banyak digunakan dalam berbagai penerapan seperti pada penyelesaian sistem persamaan, dan di artikel ini kita akan belajar mengenai Materi Transpose Matriks.
Mulai dari Pengertian dari Transpose Matriks, Rumus atau Cara Mencari Transpose Matriks dan Contoh Soal Transpose Matriks yang disertai dengan Pembahasan.
Baca Juga Rumus Perkalian Matriks dan Contoh Soal
Pengertian Transpose Matriks
Transpose Matriks adalah Matriks baru yang diperoleh dari sebuah cara menukar elemen komponen kolom menjadi elemen komponen baris ataupun sebaliknya.
Transpose Matriks sendiri dinotasikan dengan adanya pangkat huruf T seperti pada Transpose Matriks A memiliki notasi AT.
Transpose Matriks juga memiliki beberapa sifat yaitu:
- (A + B)T = (A)T + (B)T
- (AB)T = AT
- ATT = A
- (kA)T = k(AT)
Cara Mencari Transpose Matriks
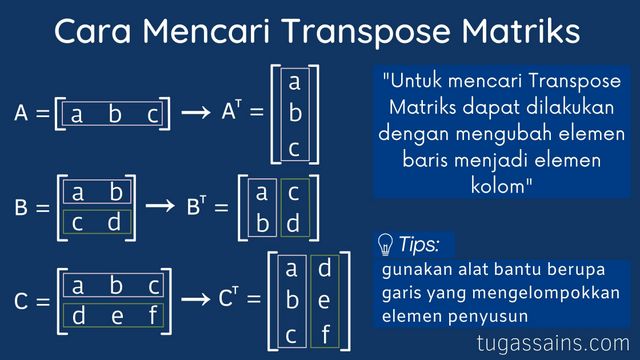
Untuk dapat mencari transpose matriks kita tidak membutuhkan cara atau rumus khusus yaitu dapat kita lakukan dengan mengubah elemen baris menjadi elemen kolom ataupun sebaliknya.
Untuk mencari transpose matriks kita dapat menggunakan bantuan garis untuk mengelompokkan berdasarkan elemen kolom ataupun baris pada kertas buram/uraian.
Namun ketika melakukan transpose matriks pada matriks persegi diperoleh matriks yang sama dengan matriks sebelumnya, itu dikatakan jenis matriks simetris (matriks simetris hanya berlaku pada matriks persegi).
Untuk dapat lebih memahami materi Transpose Matriks mari kita latih dengan Contoh Soal Pembahasan Transpose Matriks berikut.
Contoh Soal Transpose Matriks
1. Carilah Matriks Transpose dari Matriks A berikut.

Jawab: Gunakan garis bantu untuk mengelompokkan elemen baris lalu ubah elemen baris menjadi elemen kolom.

2. Dari Matriks B berbentu persegi panjang berikut carilah matriks BT!

Jawab: Cari nilai BT! dengan mengelompokkan elemen baris lalu ubah menjadi elemen kolom dengan bantuan garis yang mengelompokkan.

3. Tuliskan Matriks baru yang dihasilkan dari transpose matriks C.

Jawab: Cari matriks baru dari melakukan transpose matriks C, gunakan garis bantuan pengelompokkan elemen lalu lakukan transpose.

4. Carilah transpose matriks persegi D tersebut!

Jawab: Cari transpose matriks D atau (DT) dengan mengubah elemen baris menjadi kolom dengan bantuan garis.

5. Buktikan bahwa matriks persegi E tersebut adalah matriks simetris dengan mencari nilai ET!

Jawab: Lakukan pembuktian dengan melakukan transpose Matriks E tersebut, gunakan garis bantuan agar diperoleh transpose matriks dengan mudah.

Karena nilai matriks E sama dengan matriks ET dapat dikatakan matriks E merupakan Matriks Simetris.
Baca Juga Rumus Invers Matriks dan Contoh Soal
Semoga bermanfaat jika ada yang ingin ditanyakan silahkan bertanya pada kolom komentar dan jangan lupa bagikan, terima kasih.