Pada artikel ini berisi materi Matematika mengenai Contoh Soal Cerita SPLTV dengan Pembahasan yang mudah dan jelas sebagai bahan pembelajaran
tugassains.com – SPLTV atau Sistem Persamaan Linear Tiga Variabel merupakan salah satu persamaan linear Matematika yang memiliki tiga buah variabel didalamnya (misalkan x, y dan z). Ditiap variabel tersebut memiliki nilai penyelesaian yang pasti.
Setiap penyelesaian dapat kita cari dengan menggunakan beberapa Metode yaitu Metode Eliminasi, Metode Substitusi, Metode Grafik dan Metode Campuran.
Dan di artikel ini kita akan belajar contoh soal persamaan linear tiga variabel dalam bentuk Soal Cerita dengan Pembahasan contoh soal yang mudah di pahami
Baca Juga Cara Menyelesaikan SPLTV Metode Eliminasi
Contoh Soal Cerita SPLTV
1. Harga 3 buku tulis, 2 pensil dan 3 bolpoin adalah Rp. 15.700, dan harga 2 buku tulis dan 3 pensil adalah Rp. 9.200 sedangkan harga 4 pensil dan 3 bolpoin adalah Rp. 11.000 Jika Budi ingin mebeli 2 buku tulis, 1 pensil dan 1 bolpoin, maka Budi harus membayar sebanyak….
Jawab:
Untuk menyelesaikan Soal Cerita SPLTV seperti ini kita harus membuat persamaan dengan memisalkan variabel terlebih dahulu.
Misal: Buku = x, Pensil = y dan Bolpoin = z.
3x + 2y + 3z = 15.700 ….(1)
2x + 3y = 9.200 ….(2)
4y + 3z = 11.000 ….(3)
Ditanya: Harga 2 buku tulis, 1 pensil dan 1 bolpoin (2x + y + z = ….)?
Penyelesaian:
Kita dapat melakukan penyelesaian dengan metode campuran yaitu kita dapat melakukan eliminasi terlebih dahulu dengan mengeliminasi x dari persamaan 1 dan 2.
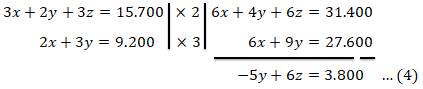
Kemudian setelah variabel tersisa y dan z kita dapat langsung mengeliminasi z dari persamaan 3 dan 4 untuk mencari nilai y.

Setelah mengetahui nilai y, lakukan substitusi nilai y ke persamaan 2 untuk mencari nilai x.
2x + 3y = 9.200
2x + 3(1.400) = 9.200
2x + 4.200 = 9.200
2x = 5.000
x = 5.000/2
x = 2.500
Dan lakukan kembali substitusi nilai y ke persamaan 3 untuk mencari nilai z.
4y + 3z = 11.000
4(1.400) + 3z = 11.000
5.600 + 3z = 11.000
3z = 5.400
z = 5.400/3
z = 1.800
Setelah mengetahui harga masing-masing mari kita jawab pertanyaan yaitu harga 2 buku tulis, 1 pensil dan 1 bolpoin (2x + y + z = ….). (x = 2.500, y = 1.400 dan z = 1.800)
2x + y + z = 2(2.500) + 1.400 + 1.800
2x + y + z = 5.000 + 1.400 + 1.800
2x + y + z = 8.200
Jadi harga 2 buku tulis, 1 pensil dan 1 bolpoin yaitu Rp. 8.200.
2. Rizki mempunyai pita hias berwarna merah, ungu dan kuning. Jumlah panjang ketiga pita hias tersebut 275 cm. Panjang pita ungu 5 cm kurang dari panjang pita kuning. Panjang pita kuning 20cm lebih dari panjang pita merah. Jika pita kuning digunakan 35cm , panjang sisa pita kuning….
Jawab:
Untuk menyelesaikan Soal Cerita SPLTV seperti ini kita harus membuat persamaan dengan memisalkan variabel terlebih dahulu agar di temukan persamaan
Misal: Pita Merah = a, Pita Ungu = b dan Pita Kuning = c.
a + b + c = 275 ….(1)
b = c – 5 ….(2)
c = a + 20 ….(3)
Ditanya: Panjang pita kuning jika digunakan 35cm (c – 25 = ….)?
Penyelesaian:
Dari persamaan tersebut kita dapat langsung mengetahui untuk menyelesaikan persamaan linear tiga variabel tersebut kita dapat menggunakan Metode Substitusi, namun kita ubah terlebih dahulu persamaan
3. Subtitusi persamaan
c = a + 20
a = c – 20 …(4)
Lakukan subtitusi persamaan 2 dan 4 ke persamaan 1 untuk mencari nilai c.
a + b + c = 275
(c – 20) + (c – 5) + c = 275
c + c + c – 20 – 5 = 275
3c – 25 = 275
3c = 275 + 25
c = 300/3
c = 100
Panjang pita kuning = 100cm maka bila digunakan 35cm yaitu
= c – 35 = 100 – 35
= 65cm
Jadi panjang sisa pita kuning yaitu sepanjang 65cm.
3. Harga 2kg jeruk dan 3kg apel adalah Rp.69.000 sedangkan harga 1kg jeruk, 2kg apel dan 1kg manggis adalah Rp. 50.000 Harga 2kg jeruk, 1kg apel dan 3kg manggis adalah Rp. 63.000. Jika Bu Via membeli jeruk, apel dan manggis masing-masing 1kg dan menyerahkan uang lima puluh ribu maka besar
kembaliannya sebesar?
Jawab:
Agar mempermudah penyelesaian dari soal cerita spltv tersebut mari kita hitung dengan mengubah ke dalam bentuk persamaan terlebih dahulu.
Misal: 1kg jeruk = x, 1kg apel = y dan 1 kg manggis = z.
2x + 3y = 69.000 ….(1)
x + 2y + z = 50.000 ….(2)
2x + y + 3z = 63.000 ….(3)
Ditanya: Kembalian membeli 1 kg jeruk, 1 kg apel dan 1 kg manggis dengan uang Rp. 50.000 (50.000 – (x + y + z)) ?
Penyelesaian:
Untuk menyelesaikan persamaan tiga variabel tersebut kita dapat menghitung dengan melakukan Metode Eliminasi.
Eliminasi z persamaan 2 dan 3 untuk menyisakan variabel x dan y

Kemudian lakukan elimininasi x dari persamaan 1 dan 4 untuk mencari nilai y.
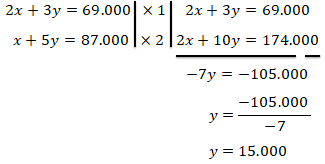
Subtitusikan nilai y = 15.000 ke persamaan 1 untuk mencari nilai x
2x + 3y = 69.000
2x + 3(15.000) = 69.000
2x + 45.000 = 69.000
2x = 24.000
x = 12.000
Kemudian lakukan subtitusi kembali x = 12.000 dan y = 15.000 ke persamaan 2 untuk mencari nilai z.
x + 2y + z = 50.000
(12.000) + 2(15.000) + z = 50.000
12.000 + 30.000 + z = 50.000
z = 8.000
Setelah mengetahui nilai x = 12.000, y = 15.000 dan z = 8.000 hitung kembalian pada pertanyaan:
Kembalian = 50.000 – (x + y + z)
Kembalian = 50.000 – (12.000 + 15.000 + 8.000)
Kembalian = 50.000 – 35.000
Kembalian = 15.000
Jadi besar kembalian dengan uang Rp. 50.000 untuk membeli 1 kg jeruk, 1 kg apel dan 1 kg manggis sebesar Rp. 15.000.
Baca Juga Cara Menyelesaikan SPLTV Metode Substitusi
Sekian terima kasih jika ada yang ditanyakan silahkan di kolom komentar atau hubungi pada halaman contact us semoga bermanfaat.




