tugassains.com – Vektor merupakan salah satu besaran yang memiliki nilai dan arah, dimana kita akan menemukan vektor pada bidang dua dimensi yaitu pada sumbu (x, y) dan juga pada bidang tiga dimensi yaitu pada sumbu (x, y, z).
Didalamnya terdapat berbagai operasi hitung seperti penjumlahan vektor, pengurangan vektor, perkalian cross vektor, perkalian dot vektor dan panjang vektor. Kemudian sifat dua vektor tegak lurus dan dua vektor saling sejajar.
Selain operasi hitung tersebut terdapat juga vektor satuan yang akan kita pelajari berikut mulai dari rumus hingga contoh soal.
 |
| Vektor Satuan |
Baca juga Besaran Skalar dan Besaran Vektor
Rumus Vektor Satuan
Bagaimana menghitung nilai vektor satuan? untuk menghitungnya kita hanya perlu membagi antara nilai vektor terhadap nilai panjang vektornya,
Pada bidang R2 atau vektor dimensi dua kita dapat menghitung dengan rumus berikut.
 |
| Rumus Vektor Satuan Bidang R2 |
Sedangkan pada bidang R3 atau vektor dimensi tiga sedikit berbeda karena memiliki tiga sumbu (x, y, z) sehingga kita menghitungnya dengan membagikan antara panjang vektor dimensi tiga dengan nilai vektornya, seperti berikut.
 |
| Rumus Vektor Satuan Bidang R3 |
Agar lebih jauh memahami yuk mari kita belajar menghitungnya dengan Contoh Soal yang disertai pembahasan berikut.
Contoh Soal Vektor Satuan
1. Carilah nilai vektor satuan a jika diketahui nilai a(6, 8) seperti berikut!
 |
| Contoh Soal Vektor Satuan |
penyelesaian:
a(6, 8)
Terletak pada bidang R2 sehingga kita dapat menghitung nilainya sebagai berikut.
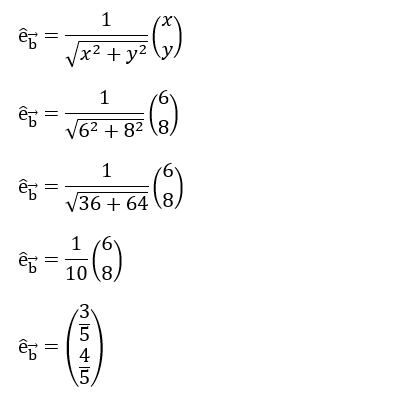
Jadi nilai vektor satuan a(3/5, 4/5).
2. Diketahui sebuah vektor b = -4i + 3j, hitunglah besar nilai vektor satuannya!
penyelesaian:
b(-4, 3)
Sama seperti contoh soal sebelumnya sehingga dapat kita hitung sesuai dengan rumus.
Jadi vektor satuan dari vektor tersebut yaitu b = -4/5i + 3/5j.
3. Diketahui sebuah vektor m = -i + 8j – 4k memiliki panjang vektor |m| = 9. Hitunglah nilai vektor satuan m yang berada pada bidang R3 tersebut!
penyelesaian:
|m| = 9
m(-1, 8, -4)
Pada permasalahan tersebut sedikit berbeda karena berada pada bidang R3 sehingga terdapat sumbu z, kemudian hitung sesuai dengan rumus yaitu membagi antara nilai vektor terhadap panjang vektor.
Jadi vektor satuan m = -1/9i + 8/9j – 4/9k.
4. Hitunglah vektor satuan dari n(2, -4, 4)!
penyelesaian:
n(2, -4, 4)
Hampir sama dengan permasalahan sebelumnya namun pada soal kita perlu menghitung terlebih dahulu panjang vektor kemudian dapat menghitung sesuai dengan rumus.
Jadi vektor satuan m bernilai n(1/3, -2/3, 2/3).
5. Sebuah titik a(-7, 4) dan titik b(5, 9) ditarik menjadi vektor ab, hitunglah besar nilai vektor satuan ab!
penyelesaian:
a(xa = -7, ya = 4)
b(xb = 5, yb = 9)
cari terlebih dahulu nilai vektor ab.
kemudian subtitusikan nilai vektor ab ke dalam rumus.
Jadi nilai vektor satuan ab (-12/13, 5/13).
Baca Juga: Proyeksi Skalar dan Proyeksi Ortogonal
Semoga bermanfaat, terima kasih.
