tugassains.com – Vektor merupakan besaran yang memiliki nilai dan arah, vektor merupakan salah satu materi yang banyak diterapkan di berbagai pelajaran yang lebih mendalam dan penerapan di kehidupan sehari-hari.
Dimana panjang vektor juga digunakan untuk saat mencari panjang proyeksi skalar dan proyeksi vektor ortogonal serta vektor satuan. Melalui artikel ini kita akan belajar menghitung menggunakan rumus dan
contoh soal pembahasan.
 |
| Panjang Vektor |
Rumus Panjang Vektor
Untuk menghitung panjang dari suatu vektor kita dapat menghitung sesuai rumus berdasarkan dimensi yaitu R2 dan R3, panjang vektor biasanya dilambangkan dengan notasi vektor yang berada pada tanda mutlak.
Jika sebuah vektor berada pada titik P(x, y) dan O(0, 0) di R2 maka:
 |
| Rumus Panjang Vektor R2 |
Jika sebuah vektor berada pada titik P(x, y, z) dan O(0, 0, 0) di R3 maka:
 |
| Rumus Panjang Vektor R3 |
Rumus Panjang Vektor antara dua titik
Ketika mempelajari vektor kita akan menemui panjang vektor antara dua titik atau jarak antara kedua vektor, sehingga kita dapat hitung dengan menggunakan rumus:
Diketahui koordinat titik P(x1, y1), Q(x2, y2) dan O(0, 0) maka panjang vektor atau jarak antara kedua titik dapat dicari dengan rumus
 |
| Rumus Panjang Vektor Dua Titik pada R2 |
Diketahui koordinat titik P(x1, y1, z1), Q(x2, y2, z2) dan O(0, 0, 0) maka panjang vektor atau jarak antara kedua titik dapat dicari dengan rumus:
 |
| Rumus Panjang Vektor Dua Titik pada R3 |
Setelah mengetahui rumus selanjutnya kita akan belajar mengasah pemahaman kita dengan memahami contoh soal pembahasa berikut.
Baca juga Vektor Tegak Lurus
Contoh Soal Panjang Vektor
1. Hitunglah panjang vektor a pada bidang R2 berikut:
 |
| Contoh Soal Panjang Vektor |
penyelesaian: a(8, 6)
Subtitusikan nilai x dan y ke dalam rumus lalu hitung untuk memperoleh hasilnya.
Jadi panjang vektor a bernilai 10.
2. Sebuah vektor pada bidang R3 yaitu e = 1 + 7j – 5k, carilah besar nilai |e|!
penyelesaian: e(1, 7, -5)
Hitung nilai |e| dengan rumus pada bidang R3 dimensi seperti berikut.
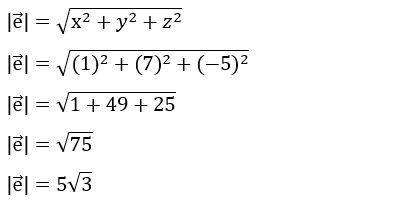
Jadi besar nilai dari |e| yaitu 5√3.
3. Diketahui a(7, -5) dan b(-3, 3) hitunglah berapa nilai panjang vektor ab tersebut?
penyelesaian:
a (7, -5)
b (3, 3)
subtiusikan nilai a(x1 = 7, y1 = -5) dan vektor b(x2 = 3, y2 = 3) ke dalam rumus.
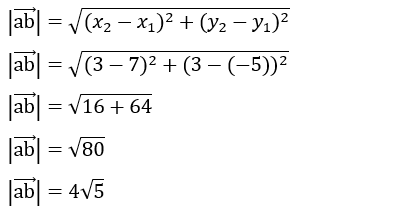
Jadi panjang vektor ab sebesar 4√5.
4. Diketahui m = -5i + 3j – 5k dan n = 7i – 3j + 5k, hitunglah
nilai |mn|!
penyelesaian:
m(x1 = -5, y1 = 3, z1 = -5)
n(x2 = 7, y2 = -3, z2 = 5)
Dengan menggunakan rumus panjang vektor pada bidang R3 kita dapat mengetahui nilai |mn|.
Jadi panjang vektor de yaitu bernilai 2√70.
Baca juga Besaran Skalar dan Besaran Vektor
Semoga bermanfaat, terima kasih.
