Pada artikel ini membahas mengenai Pengertian dan Contoh Soal Sistem Persamaan Linear Dua Variabel dalam
bentuk Pecahan dengan penyelesaian serta penjelasan yang mudah dipahami.
 |
| Contoh Soal SPLDV Dalam Bentuk Pecahan beserta Penyelesaian |
tugassains.com – SPLDV (Sistem Persamaan Linear Dua Variabel) adalah
suatu persamaan matematika merupakan dua persamaan linear yang memiliki dua
variabel di masing-masing persamaannya (seperti x dan y).
Bentuk umum dari SPLDV yaitu:
ax + by = c
Keterangan:
a dan b = koefisien dari variabel pada persamaan
x
dan y = variabel dari persamaan
*perlu diingat bahwa Sistem Persamaan Linear Dua Variabel hanya memiliki dua
variabel di persamaan nya, sesuai namanya Sistem Persamaan Linear Dua
Variabel.
c = konstanta dari persamaan
Dan pada kesempatan ini kita akan belajar mengenai cara mencari penyelesaian
atau nilai dari Sistem Persamaan Linear Dua Variabel dalam bentuk pecahan,
yang dibahas dalam contoh soal dengan penjelasan dan cara yang mudah.
Baca Juga Cara Menyelesaikan SPLDV Metode Substitusi
Contoh Soal SPLDV Dalam Bentuk Pecahan
1. Penyelesaian dari Sistem Persamaan Linear Dua Variabel dalam bentuk
pecahan tersebut.
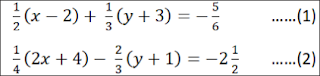
Jawab:
Untuk penyelesaian langkah pertama yaitu mengubah bentuk persamaan dari yang
sebelumnya pecahan menjadi bukan dalam pecahan yaitu dengan mengalikan ke kpk
dari masing-masing penyebutnya.
Tips cari kpk: Cari kpk dari penyebutnya misal kpk pada persamaan 1 yaitu 6
dari penyebut 2, 3, dan 6.
pada persamaan 1 memiliki penyebut 2, 3 dan 6 jadi kpk yaitu 6 sehingga:
dan pada persamaan 2 memiliki penyebut 4, 3 dan 2 jadi kpk yaitu 12 sehingga:
Jadi setelah mengubah dari bentuk pecahan ke bentuk biasa langkah selanjutnya
adalah menggunakan metode eliminasi untuk mencari nilai variabel x dan y dari
persamaan.
Eliminasi variabel x dari persamaan 1 dan 2
Jadi diperoleh nilai y = 2, setelah itu cari nilai x dengan substitusi
y = 2 ke persamaan 1 untuk mencari nilai x dari persamaan
Diperoleh nilai x = -3 dari subtitusi y = 2 ke dalam persamaan.
Jadi Himpunan Penyelesaian atau HP dari Sistem Persamaan Linear Dua Variabel
dalam bentuk pecahan tersebut HP x = -3 dan y = 2.
2. Tentukan Nilai x dan y dari Persamaan berikut:
Penyelesaian:
Langkah pertama yaitu sama dengan nomor 1 yaitu dengan menyederhanakan
persamaan yang semula berbentuk pecahan menjadi persamaan biasa dengan
mengalikan KPK dari masing-masing penyebut persamaan.
Pada persamaan 1 penyebut 4 dan 3 memiliki KPK 12 sehingga kalikan dengan 12:
Pada persamaan 1 penyebut 4 dan 3 memiliki KPK 12 sehingga kalikan dengan 12:
Setelah itu eliminasi x dari persamaan 1 dan 2 untuk mencari nilai y dari
persamaan:
Sehingga di peroleh nilai y = -6 kemudian subtitusi y = -6 untuk
mencari nilai x ke persamaan 1
Setelah disubtitusi y = -6 diperoleh nilai x dari persamaan yaitu
sebesar x = 12.
Jadi nilai x dan y dari Sistem Persamaan Linear Dua Variabel dalam bentuk
pecahan tersebut bernilai x = 12 dan y = -6.
Baca Juga Cara Menyelesaikan SPLDV Metode Eliminasi
Semoga bermanfaat jika ada yang ingin ditanyakan silahkan tanya di kolom
komentar dan jangan lupa bagikan.